COMP 356 Programming Language Structures Notes for Chapter 15
... • strict evaluation – is easier to implement – is more efficient in many cases • lazy evaluation – is more efficient in some cases (if some parameters are never used) – permits infinite data structures Scheme programmers can define lazy functions using macros or thunks (as in pass-by-name). Other im ...
... • strict evaluation – is easier to implement – is more efficient in many cases • lazy evaluation – is more efficient in some cases (if some parameters are never used) – permits infinite data structures Scheme programmers can define lazy functions using macros or thunks (as in pass-by-name). Other im ...
Slide 1
... To move n disks from A to C using B as auxiliary 1.If n==1, move single disk from A to C. 2.Move the top n-1 disks from A to B using C as auxiliary. 3.Move the remaining disk from A to C. 4.Move the n-1 disks from B to C, using A as auxiliary. • Here if n==1, step1 will produce a correct solution. • ...
... To move n disks from A to C using B as auxiliary 1.If n==1, move single disk from A to C. 2.Move the top n-1 disks from A to B using C as auxiliary. 3.Move the remaining disk from A to C. 4.Move the n-1 disks from B to C, using A as auxiliary. • Here if n==1, step1 will produce a correct solution. • ...
recursively
... How many students total are directly behind you in your "column" of the classroom? – You have poor vision, so you can see only the people right next to you. So you can't just look back and count. – But you are allowed to ask questions of the person next to you. ...
... How many students total are directly behind you in your "column" of the classroom? – You have poor vision, so you can see only the people right next to you. So you can't just look back and count. – But you are allowed to ask questions of the person next to you. ...
PPT
... Functional prog better than imperative programming Easier to reason about functional programs More efficient due to parallelism ...
... Functional prog better than imperative programming Easier to reason about functional programs More efficient due to parallelism ...
View
... Every time a function gets called, Python creates a new function frame, which contains the function's local variables and parameters. For a recursive function, there might be more than one frame on the stack at the same time. This figure shows a stack diagram for countdown called with n = 3: ...
... Every time a function gets called, Python creates a new function frame, which contains the function's local variables and parameters. For a recursive function, there might be more than one frame on the stack at the same time. This figure shows a stack diagram for countdown called with n = 3: ...
Functional Imperative Style
... on y to show that f 0 returns the square of y, for non-negative y, as follows. Base case If y = 0, then f 0 0 0 0 returns 0, by the definition of f 0 . This is correct, for 02 = 0. Induction step Assume for y = m the function call f 0 m x m returns x with x = m2 . We have to show that for y = m + 1, ...
... on y to show that f 0 returns the square of y, for non-negative y, as follows. Base case If y = 0, then f 0 0 0 0 returns 0, by the definition of f 0 . This is correct, for 02 = 0. Induction step Assume for y = m the function call f 0 m x m returns x with x = m2 . We have to show that for y = m + 1, ...
bYTEBoss control
... Knuth, Structured Prog. with go to Statements • You can use goto, but do so in structured way … ...
... Knuth, Structured Prog. with go to Statements • You can use goto, but do so in structured way … ...
Functional Programming, Parametricity, Types
... theorems about this function can be reliably constructed ...
... theorems about this function can be reliably constructed ...
functional form
... • Lambda notation is used to specify functions and function definitions. Function applications and data have the same form. e.g., If the list (A B C) is interpreted as data it is a simple list of three atoms, A, B, and C If it is interpreted as a function application, it means that the function name ...
... • Lambda notation is used to specify functions and function definitions. Function applications and data have the same form. e.g., If the list (A B C) is interpreted as data it is a simple list of three atoms, A, B, and C If it is interpreted as a function application, it means that the function name ...
Recursion 2
... • Another way to characterize recursive methods is by the way in which the recursion grows. The two basic ways are "linear" and "tree." • A recursive method is said to be linearly recursive when no pending operation involves another recursive call to the method. • For example, the factorial method i ...
... • Another way to characterize recursive methods is by the way in which the recursion grows. The two basic ways are "linear" and "tree." • A recursive method is said to be linearly recursive when no pending operation involves another recursive call to the method. • For example, the factorial method i ...
Functional programming
... Can be emulated in traditional languages such as C++ and java: expressions in general behave like pure functions; many routines without using global variables behave like pure functions. ...
... Can be emulated in traditional languages such as C++ and java: expressions in general behave like pure functions; many routines without using global variables behave like pure functions. ...
fund
... enq (elt, q) returns queue with elt at back of q front (q) returns front element of q deq (q) returns q with front element removed ...
... enq (elt, q) returns queue with elt at back of q front (q) returns front element of q deq (q) returns q with front element removed ...
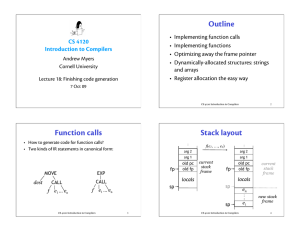
Finishing code generation
... • Given instruction, replace every temporary in instruction with one of three registers e[acd]x • Add mov instructions before instruction to load registers properly • Add mov instructions after instruction to put data back onto stack (if necessary) ...
... • Given instruction, replace every temporary in instruction with one of three registers e[acd]x • Add mov instructions before instruction to load registers properly • Add mov instructions after instruction to put data back onto stack (if necessary) ...
Functional Programming Basics
... • A function f from domain A to co-domain B, denoted f : A -> B, is a map that associates with every element a in A, a unique element b in B, denoted f(a). – Cf. Relation, multi-valued function, partial function, … – In mathematics, the term “function” usually refers to a total function; in computer ...
... • A function f from domain A to co-domain B, denoted f : A -> B, is a map that associates with every element a in A, a unique element b in B, denoted f(a). – Cf. Relation, multi-valued function, partial function, … – In mathematics, the term “function” usually refers to a total function; in computer ...
Lisp, Then and Now
... For a function: The arguments are evaluated and their values passed to the function ...
... For a function: The arguments are evaluated and their values passed to the function ...
Joy: Forth`s Functional Cousin
... where "Lx" is sometimes written "\x" or "lambda x" of "fn x". The expression on the right side of the definition then is to be read as "the function of one argument x which yields the value x * x". An expression like that is known as a lambda abstraction. Almost all programming languages use such a ...
... where "Lx" is sometimes written "\x" or "lambda x" of "fn x". The expression on the right side of the definition then is to be read as "the function of one argument x which yields the value x * x". An expression like that is known as a lambda abstraction. Almost all programming languages use such a ...
Fundamentals
... Functional programming: Example 1 Devise a representation for stacks and implementations for functions push (elt, stk) returns stack with elt on top of stk top (stk) returns top element of stk pop (stk) returns stk with top element removed ...
... Functional programming: Example 1 Devise a representation for stacks and implementations for functions push (elt, stk) returns stack with elt on top of stk top (stk) returns top element of stk pop (stk) returns stk with top element removed ...
Functional Programming
... It is ambiguous : we do not know which names are parameters and which ones are global “lambda expressions” come in hand (mapcar ‘(lambda (x) (cons val x)) L) ...
... It is ambiguous : we do not know which names are parameters and which ones are global “lambda expressions” come in hand (mapcar ‘(lambda (x) (cons val x)) L) ...
Functional Programming www.AssignmentPoint.com In computer
... recursion. Recursive functions invoke themselves, allowing an operation to be performed over and over until the base case is reached. Though some recursion requires maintaining a stack, tail recursion can be recognized and optimized by a compiler into the same code used to implement iteration in imp ...
... recursion. Recursive functions invoke themselves, allowing an operation to be performed over and over until the base case is reached. Though some recursion requires maintaining a stack, tail recursion can be recognized and optimized by a compiler into the same code used to implement iteration in imp ...
function
... by replacing all free occurrences of x in M by N. 2. Otherwise, assume that the variable y is free in N and bound in M. Consistently replace the binding and the corresponding bound occurrences of y in M by a new variable (say u). Repeat renaming bound variables in M until the condition in step 1 app ...
... by replacing all free occurrences of x in M by N. 2. Otherwise, assume that the variable y is free in N and bound in M. Consistently replace the binding and the corresponding bound occurrences of y in M by a new variable (say u). Repeat renaming bound variables in M until the condition in step 1 app ...
CSC 533: Programming Languages Spring 2015
... unlike arrays, lists do not have to store items of same type/size do not have to be stored contiguously do not have to provide random access § all computation is performed by applying functions to arguments in pure LISP: no variables, no assignments, no iteration § functions and function calls a ...
... unlike arrays, lists do not have to store items of same type/size do not have to be stored contiguously do not have to provide random access § all computation is performed by applying functions to arguments in pure LISP: no variables, no assignments, no iteration § functions and function calls a ...
ppt - Dave Reed
... each full-recursive call requires a new activation record on the run-time stack with tail-recursion, don't need to retain current activation record when make call can discard the current activation record, push record for new recursive call thus, no limit on recursion depth (each recursive call ...
... each full-recursive call requires a new activation record on the run-time stack with tail-recursion, don't need to retain current activation record when make call can discard the current activation record, push record for new recursive call thus, no limit on recursion depth (each recursive call ...