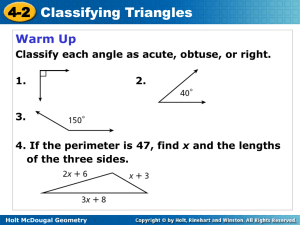
Geo 2.1 Using Inductive Reasoning to Make Conjectures
... Using Inductive Reasoning to 2-1 Make Conjectures When several examples form a pattern and you assume the pattern will continue, you are applying inductive reasoning. Inductive reasoning is the process of reasoning that a rule or statement is true because specific cases are true. You may use induct ...
... Using Inductive Reasoning to 2-1 Make Conjectures When several examples form a pattern and you assume the pattern will continue, you are applying inductive reasoning. Inductive reasoning is the process of reasoning that a rule or statement is true because specific cases are true. You may use induct ...
1-3 Measuring and Constructing Angles
... with a common endpoint called the vertex (plural: vertices). You can name an angle several ways: by its vertex, by a point on each ray and the vertex, or by a number. ...
... with a common endpoint called the vertex (plural: vertices). You can name an angle several ways: by its vertex, by a point on each ray and the vertex, or by a number. ...
Section 7.1 Powerpoint
... 1. If ∆QRS ∆ZYX, identify the pairs of congruent angles and the pairs of congruent sides. Q Z; R Y; S X; QR ZY; RS YX; QS ZX Solve each proportion. ...
... 1. If ∆QRS ∆ZYX, identify the pairs of congruent angles and the pairs of congruent sides. Q Z; R Y; S X; QR ZY; RS YX; QS ZX Solve each proportion. ...
similar polygons
... 1. If ∆QRS ∆ZYX, identify the pairs of congruent angles and the pairs of congruent sides. Q Z; R Y; S X; QR ZY; RS YX; QS ZX Solve each proportion. ...
... 1. If ∆QRS ∆ZYX, identify the pairs of congruent angles and the pairs of congruent sides. Q Z; R Y; S X; QR ZY; RS YX; QS ZX Solve each proportion. ...
7-2
... 1. If ∆QRS ∆ZYX, identify the pairs of congruent angles and the pairs of congruent sides. Q Z; R Y; S X; QR ZY; RS YX; QS ZX Solve each proportion. ...
... 1. If ∆QRS ∆ZYX, identify the pairs of congruent angles and the pairs of congruent sides. Q Z; R Y; S X; QR ZY; RS YX; QS ZX Solve each proportion. ...
Which transformation maps the solid figure onto the dashed figure
... For k = 1, P1 is on m; for k > 1, P1 is in the shaded half-plane; for 0 < k < 1, P1 is in the non-shaded half-plane. ...
... For k = 1, P1 is on m; for k > 1, P1 is in the shaded half-plane; for 0 < k < 1, P1 is in the non-shaded half-plane. ...
Holt McDougal Geometry
... The converse of a theorem is not automatically true. If it is true, it must be stated as a postulate or proved as a separate theorem. ...
... The converse of a theorem is not automatically true. If it is true, it must be stated as a postulate or proved as a separate theorem. ...
4-5 Triangle Congruence: SSS and SAS
... 4-5 Triangle Congruence: SSS and SAS It can also be shown that only two pairs of congruent corresponding sides are needed to prove the congruence of two triangles if the included angles are also congruent. ...
... 4-5 Triangle Congruence: SSS and SAS It can also be shown that only two pairs of congruent corresponding sides are needed to prove the congruence of two triangles if the included angles are also congruent. ...
Hyperbolic Geometry in the High School Geometry Classroom
... deduction, prove theorems, and critique arguments made by others”(2000, p. 308). ...
... deduction, prove theorems, and critique arguments made by others”(2000, p. 308). ...
Inductive reasoning
... three times higher than the greatest humpbackwhale spout (9 ft). Possible conjectures: The height of a blue whale’s spout is about three times greater than a humpback whale’s spout. The height of a blue-whale’s spout is greater than a humpback whale’s spout. ...
... three times higher than the greatest humpbackwhale spout (9 ft). Possible conjectures: The height of a blue whale’s spout is about three times greater than a humpback whale’s spout. The height of a blue-whale’s spout is greater than a humpback whale’s spout. ...
7.1 Similar Polygons PP
... 1. If ∆QRS ∆ZYX, identify the pairs of congruent angles and the pairs of congruent ...
... 1. If ∆QRS ∆ZYX, identify the pairs of congruent angles and the pairs of congruent ...
Algebraic geometry

Algebraic geometry is a branch of mathematics, classically studying zeros of multivariate polynomials. Modern algebraic geometry is based on the use of abstract algebraic techniques, mainly from commutative algebra, for solving geometrical problems about these sets of zeros.The fundamental objects of study in algebraic geometry are algebraic varieties, which are geometric manifestations of solutions of systems of polynomial equations. Examples of the most studied classes of algebraic varieties are: plane algebraic curves, which include lines, circles, parabolas, ellipses, hyperbolas, cubic curves like elliptic curves and quartic curves like lemniscates, and Cassini ovals. A point of the plane belongs to an algebraic curve if its coordinates satisfy a given polynomial equation. Basic questions involve the study of the points of special interest like the singular points, the inflection points and the points at infinity. More advanced questions involve the topology of the curve and relations between the curves given by different equations.Algebraic geometry occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex analysis, topology and number theory. Initially a study of systems of polynomial equations in several variables, the subject of algebraic geometry starts where equation solving leaves off, and it becomes even more important to understand the intrinsic properties of the totality of solutions of a system of equations, than to find a specific solution; this leads into some of the deepest areas in all of mathematics, both conceptually and in terms of technique.In the 20th century, algebraic geometry has split into several subareas. The main stream of algebraic geometry is devoted to the study of the complex points of the algebraic varieties and more generally to the points with coordinates in an algebraically closed field. The study of the points of an algebraic variety with coordinates in the field of the rational numbers or in a number field became arithmetic geometry (or more classically Diophantine geometry), a subfield of algebraic number theory. The study of the real points of an algebraic variety is the subject of real algebraic geometry. A large part of singularity theory is devoted to the singularities of algebraic varieties. With the rise of the computers, a computational algebraic geometry area has emerged, which lies at the intersection of algebraic geometry and computer algebra. It consists essentially in developing algorithms and software for studying and finding the properties of explicitly given algebraic varieties.Much of the development of the main stream of algebraic geometry in the 20th century occurred within an abstract algebraic framework, with increasing emphasis being placed on ""intrinsic"" properties of algebraic varieties not dependent on any particular way of embedding the variety in an ambient coordinate space; this parallels developments in topology, differential and complex geometry. One key achievement of this abstract algebraic geometry is Grothendieck's scheme theory which allows one to use sheaf theory to study algebraic varieties in a way which is very similar to its use in the study of differential and analytic manifolds. This is obtained by extending the notion of point: In classical algebraic geometry, a point of an affine variety may be identified, through Hilbert's Nullstellensatz, with a maximal ideal of the coordinate ring, while the points of the corresponding affine scheme are all prime ideals of this ring. This means that a point of such a scheme may be either a usual point or a subvariety. This approach also enables a unification of the language and the tools of classical algebraic geometry, mainly concerned with complex points, and of algebraic number theory. Wiles's proof of the longstanding conjecture called Fermat's last theorem is an example of the power of this approach.