Chapter Objectives - Jacksonville University
... To learn how to use a tree to represent a hierarchical organization of information To learn how to use recursion to process trees To understand the different ways of traversing a tree To understand the difference between binary trees, binary search trees, and heaps ...
... To learn how to use a tree to represent a hierarchical organization of information To learn how to use recursion to process trees To understand the different ways of traversing a tree To understand the difference between binary trees, binary search trees, and heaps ...
Binary tree
... A full binary tree with height k is a binary tree which has 2k+1 - 1 nodes. A complete binary tree with height k is a binary tree which has maximum number of nodes possible in levels 0 through k -1, and in (k -1)’th level all nodes with children are selected from left to right. Complete binary tree ...
... A full binary tree with height k is a binary tree which has 2k+1 - 1 nodes. A complete binary tree with height k is a binary tree which has maximum number of nodes possible in levels 0 through k -1, and in (k -1)’th level all nodes with children are selected from left to right. Complete binary tree ...
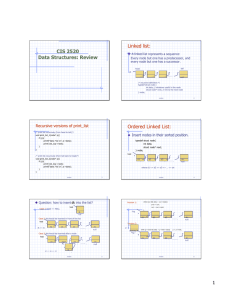
Data Structure and Algorithm Analysis part 2
... such as constants or variable names The other nodes contain operators. This particular tree happens to be binary, because all of the operations are binary It is possible for nodes to have more than two children. It is also possible for a node to have only one child, such as unary minus operator We c ...
... such as constants or variable names The other nodes contain operators. This particular tree happens to be binary, because all of the operations are binary It is possible for nodes to have more than two children. It is also possible for a node to have only one child, such as unary minus operator We c ...