MATH 105: Finite Mathematics 2
... Matrix Multiplication If we know how to multiply a row vector by a column vector, we can use that to define matrix multiplication in general. Matrix Multiplication If A is an m × n matrix and B is an n × k matrix, then the produce AB is defined to be the m × k matrix whose entry in the ith row, jth ...
... Matrix Multiplication If we know how to multiply a row vector by a column vector, we can use that to define matrix multiplication in general. Matrix Multiplication If A is an m × n matrix and B is an n × k matrix, then the produce AB is defined to be the m × k matrix whose entry in the ith row, jth ...
On Approximate Robust Counterparts of Uncertain Semidefinite and
... `=1 , {Y` ∈ S }`=M +1 . Consequently, (AR[ρ]) is equivalent to the semidefinite program of minimizing the objective f T x under the constraints (11). Note that the resulting problem (A[ρ]) is typically much better suited for numerical processing than (AR[ρ]). Indeed, the first M of the m × m matrix ...
... `=1 , {Y` ∈ S }`=M +1 . Consequently, (AR[ρ]) is equivalent to the semidefinite program of minimizing the objective f T x under the constraints (11). Note that the resulting problem (A[ρ]) is typically much better suited for numerical processing than (AR[ρ]). Indeed, the first M of the m × m matrix ...
Quizlet - Practice Vocabulary here
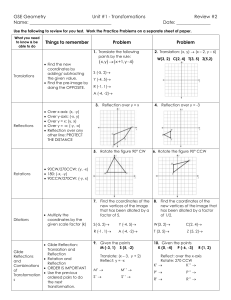
... Translation: Moving a figure vertically, horizontally, or both directions without rotating or changing the size; a slide. Center of rotation: The point around which a figure is rotated. Line of reflection: The line over which a pre-image is reflected to create a new image. Reflection: A type of tran ...
... Translation: Moving a figure vertically, horizontally, or both directions without rotating or changing the size; a slide. Center of rotation: The point around which a figure is rotated. Line of reflection: The line over which a pre-image is reflected to create a new image. Reflection: A type of tran ...