Linear Maps - People Pages - University of Wisconsin
... Example 1.18. Find a basis of the kernel and image in example (1.4). Recall that T (x1 , x2 , x3 ) = (3x1 − x3 , 5x1 + 2x2 − 4x3 ), so (x1 , x2 , x3 , x4 ) ∈ ker(T ) if and only if 3x1 − x3 = 0 5x1 + 2x2 − 4x3 = 0. We already know how to solve this system of equations. We can rewrite the solution in ...
... Example 1.18. Find a basis of the kernel and image in example (1.4). Recall that T (x1 , x2 , x3 ) = (3x1 − x3 , 5x1 + 2x2 − 4x3 ), so (x1 , x2 , x3 , x4 ) ∈ ker(T ) if and only if 3x1 − x3 = 0 5x1 + 2x2 − 4x3 = 0. We already know how to solve this system of equations. We can rewrite the solution in ...
On the energy and spectral properties of the he matrix of hexagonal
... determine the characterization of hexagonal systems from the spectral radius of the He matrix. In Section 3, we discuss the number of eigenvalues equal to zero of the He matrix of a hexagonal system. In Section 4, we obtain a relation between the number of triangles and the eigenvalues of the He mat ...
... determine the characterization of hexagonal systems from the spectral radius of the He matrix. In Section 3, we discuss the number of eigenvalues equal to zero of the He matrix of a hexagonal system. In Section 4, we obtain a relation between the number of triangles and the eigenvalues of the He mat ...
Extremal properties of ray-nonsingular matrices
... each column of DEB is still strongly balanced. Let  be an arbitrary angle and let F be the strict complex signing de ned by F = DE ⊕ [ei ]. Each of the columns, 1 through m of F A[hm + 1i; hm + 1i] is balanced. It is easy to verify that there exists a choice of  such that the (m + 1)th column ...
... each column of DEB is still strongly balanced. Let  be an arbitrary angle and let F be the strict complex signing de ned by F = DE ⊕ [ei ]. Each of the columns, 1 through m of F A[hm + 1i; hm + 1i] is balanced. It is easy to verify that there exists a choice of  such that the (m + 1)th column ...
Matrices in Matlab
... Assigning to arrays and subarrays • Note that in the last example, the memory required to store the new matrix will not "fit into" the old space occupied by the original matrix. • Matlab will handle any memory allocation needed to make matrices fit. • Matlab handles assignment to subarrays and array ...
... Assigning to arrays and subarrays • Note that in the last example, the memory required to store the new matrix will not "fit into" the old space occupied by the original matrix. • Matlab will handle any memory allocation needed to make matrices fit. • Matlab handles assignment to subarrays and array ...
Orthogonal Matrices - TTU Math Department
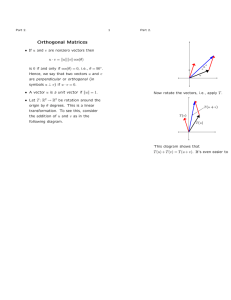
... for all vectors v . If A and B are orthogonal, so is AB . If A is orthogonal, so is A−1 . Clearly I is orthogonal.. Rotation matrices are orthogonal. The set of orthogonal 2 × 2 matrices is denoted by O(2). ...
... for all vectors v . If A and B are orthogonal, so is AB . If A is orthogonal, so is A−1 . Clearly I is orthogonal.. Rotation matrices are orthogonal. The set of orthogonal 2 × 2 matrices is denoted by O(2). ...