Lesson13 - Purdue Math
... The imaginary unit i is defined by i 1, where i 2 1 . A square root of a negative number can be represented using i in the following manner. 36 36 1 6i Ex 1: Write each number using the imaginary unit. ...
... The imaginary unit i is defined by i 1, where i 2 1 . A square root of a negative number can be represented using i in the following manner. 36 36 1 6i Ex 1: Write each number using the imaginary unit. ...
PDF
... In the period strip (1), we have one solution z1 and one solution z2 , both obtained with the value n = 0 (except z2 in the case ϕ = −π with n = −1). In (1), the points z1 and z2 are situated symmetrically with respect the origin. In the cases w = 1 and w = −1, the equation (2) has double roots z = ...
... In the period strip (1), we have one solution z1 and one solution z2 , both obtained with the value n = 0 (except z2 in the case ϕ = −π with n = −1). In (1), the points z1 and z2 are situated symmetrically with respect the origin. In the cases w = 1 and w = −1, the equation (2) has double roots z = ...
Impossible, Imaginary, Useful Complex Numbers
... Impossible, Imaginary, Useful Complex Numbers Ch. 17 Chris Conover & Holly Baust ...
... Impossible, Imaginary, Useful Complex Numbers Ch. 17 Chris Conover & Holly Baust ...
Lab 7 - Electronic Filters (C and G Sections Only)
... EG1003: Introduction to Engineering and Design ...
... EG1003: Introduction to Engineering and Design ...
lesson - Garnet Valley School District
... Big Idea #3: A logarithmic function is the inverse of an exponential function. You can identify an inverse function by comparing its graph to the graph of the original function. The two graphs are a reflection of each other across the line y = x. Exponential function: f (x) = bx The base b is any nu ...
... Big Idea #3: A logarithmic function is the inverse of an exponential function. You can identify an inverse function by comparing its graph to the graph of the original function. The two graphs are a reflection of each other across the line y = x. Exponential function: f (x) = bx The base b is any nu ...
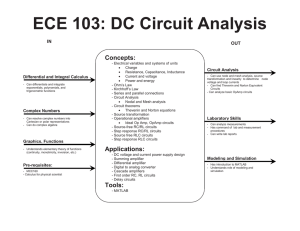
ECE 103: DC Circuit Analysis Concepts: IN
... - Can use node and mesh analysis, source transformation and linearity to determine node voltage and loop currents - Can find Thevenin and Norton Equivalent ...
... - Can use node and mesh analysis, source transformation and linearity to determine node voltage and loop currents - Can find Thevenin and Norton Equivalent ...
91577 Apply the algebra of complex numbers in solving
... forming and using a model; and also relating findings to a context, or communicating thinking using appropriate mathematical statements. Extended abstract thinking involves one or more of: devising a strategy to investigate or solve a problem identifying relevant concepts in context developi ...
... forming and using a model; and also relating findings to a context, or communicating thinking using appropriate mathematical statements. Extended abstract thinking involves one or more of: devising a strategy to investigate or solve a problem identifying relevant concepts in context developi ...
Precalculus Algebra
... Course Description This course emphasizes the algebra of functions – including polynomial, rational, exponential, and logarithmic functions. The course also covers systems of equations and inequalities, quadratic inequalities, and the binomial theorem. Additional topics may include matrices, Cramer’ ...
... Course Description This course emphasizes the algebra of functions – including polynomial, rational, exponential, and logarithmic functions. The course also covers systems of equations and inequalities, quadratic inequalities, and the binomial theorem. Additional topics may include matrices, Cramer’ ...
Mathematics of radio engineering

The mathematics of radio engineering is the mathematical description by complex analysis of the electromagnetic theory applied to radio. Waves have been studied since ancient times and many different techniques have developed of which the most useful idea is the superposition principle which apply to radio waves. The Huygen's principle, which says that each wavefront creates an infinite number of new wavefronts that can be added, is the base for this analysis.