Look at notes for first lectures in other courses
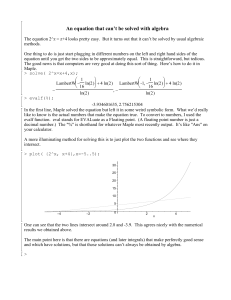
... (3) For any k, the coefficient of x^k in (1+xf(x))*r (1+xf(x))*s is a polynomial P_k(r,s) of degree k in r and s. E.g., for k=2, it’s [1][s(s-1)/2]+[r][s]+[r(r-1)/2][1]. Likewise the coefficient of x^k in (1+xf(x))*(r+s) is a polynomial Q_k(r,s) of degree k in r and s. We know that P_k(r,s) = Q_k(r, ...
... (3) For any k, the coefficient of x^k in (1+xf(x))*r (1+xf(x))*s is a polynomial P_k(r,s) of degree k in r and s. E.g., for k=2, it’s [1][s(s-1)/2]+[r][s]+[r(r-1)/2][1]. Likewise the coefficient of x^k in (1+xf(x))*(r+s) is a polynomial Q_k(r,s) of degree k in r and s. We know that P_k(r,s) = Q_k(r, ...
Graphing Linear Equations
... Linear Equation in Two Variables: An equation that can be written in the form ______________________, where A, B, and C are real numbers. The graph is a straight line. Examples of Linear Equations: ...
... Linear Equation in Two Variables: An equation that can be written in the form ______________________, where A, B, and C are real numbers. The graph is a straight line. Examples of Linear Equations: ...
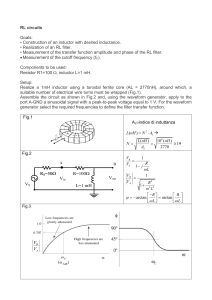
Experiment 2 R-L-C Circuits
... frequency is varied from 10 Hz to 100 KHz. Measure the phase relationship between the voltage across R and the driving source. Measure the Q of the circuit using the half power points and the resonant frequency, ωo. Compare all measurements with design calculations. ...
... frequency is varied from 10 Hz to 100 KHz. Measure the phase relationship between the voltage across R and the driving source. Measure the Q of the circuit using the half power points and the resonant frequency, ωo. Compare all measurements with design calculations. ...
Exam Review Topics
... Solving Systems (show solutions as ordered pairs) Graphing Substitution Elimination Honors topic-Cramer’s Rule (set up coefficient matrix and substitute your constants in place of the variable you’re solving for in numerator) ...
... Solving Systems (show solutions as ordered pairs) Graphing Substitution Elimination Honors topic-Cramer’s Rule (set up coefficient matrix and substitute your constants in place of the variable you’re solving for in numerator) ...
Section H2: Preliminary Material
... Rather than try to include all the effects of all possible capacitances at one time, which is virtually impossible to solve without a computer, we are going to break up the analysis into separate steps involving the low and high frequency regions and input and output circuits. For the low to midfreq ...
... Rather than try to include all the effects of all possible capacitances at one time, which is virtually impossible to solve without a computer, we are going to break up the analysis into separate steps involving the low and high frequency regions and input and output circuits. For the low to midfreq ...
Mathematics of radio engineering

The mathematics of radio engineering is the mathematical description by complex analysis of the electromagnetic theory applied to radio. Waves have been studied since ancient times and many different techniques have developed of which the most useful idea is the superposition principle which apply to radio waves. The Huygen's principle, which says that each wavefront creates an infinite number of new wavefronts that can be added, is the base for this analysis.