Full text
... Notice that we have put one hi subscript on BU and one ai subscript on AU. Now if we applied B twice, BBU = {ubb} would have two successive Z?-subscripts, and we could record how many ^-subscripts occurred by how many times we applied the B transform. Thus, a sequence of A and B transforms gives us ...
... Notice that we have put one hi subscript on BU and one ai subscript on AU. Now if we applied B twice, BBU = {ubb} would have two successive Z?-subscripts, and we could record how many ^-subscripts occurred by how many times we applied the B transform. Thus, a sequence of A and B transforms gives us ...
EET422 EMC intro 2008-2009 msw
... Lack of Mathematical rigour should not diminish the importance of the subject as Maxwell’s work was based on Michael Faraday’s ‘lines of force’ experimental observations. Maxwell discovered that electric and magnetic fields were intrinsically related with or without a conductive path for electrons. ...
... Lack of Mathematical rigour should not diminish the importance of the subject as Maxwell’s work was based on Michael Faraday’s ‘lines of force’ experimental observations. Maxwell discovered that electric and magnetic fields were intrinsically related with or without a conductive path for electrons. ...
Applied Math 9 are two ways to describe a line. If the line is not
... of n-dimensional vectors is linearly dependent when there are P real numbers faj ; j = 1; :::; J g, not all of which are zero, such that Jj=1 aj vj = 0. When a set of vectors are linearly dependent, one of the vectors can be written as a sum of the other vectors times appropriate constants. If vecto ...
... of n-dimensional vectors is linearly dependent when there are P real numbers faj ; j = 1; :::; J g, not all of which are zero, such that Jj=1 aj vj = 0. When a set of vectors are linearly dependent, one of the vectors can be written as a sum of the other vectors times appropriate constants. If vecto ...
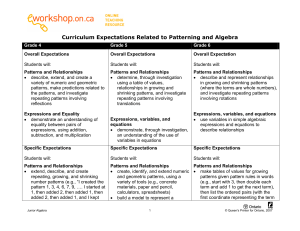
Scope and Sequence K
... (1) formulating and reasoning about expressions and equations, including modeling an association in bivariate data with a linear equation, and solving linear equations and systems of linear equations; (2) grasping the concept of a function and using functions to describe quantitative relationships; ...
... (1) formulating and reasoning about expressions and equations, including modeling an association in bivariate data with a linear equation, and solving linear equations and systems of linear equations; (2) grasping the concept of a function and using functions to describe quantitative relationships; ...
Full text
... which shows that E. is commutative as well under matrix multiplication. By an application of Eq. (11), the sums of the generalized order-k Fibonacci numbers satisfy the following recurrence relation: ...
... which shows that E. is commutative as well under matrix multiplication. By an application of Eq. (11), the sums of the generalized order-k Fibonacci numbers satisfy the following recurrence relation: ...
Mathematics of radio engineering

The mathematics of radio engineering is the mathematical description by complex analysis of the electromagnetic theory applied to radio. Waves have been studied since ancient times and many different techniques have developed of which the most useful idea is the superposition principle which apply to radio waves. The Huygen's principle, which says that each wavefront creates an infinite number of new wavefronts that can be added, is the base for this analysis.