Coordinate Algebra to Geometry Transition Packet
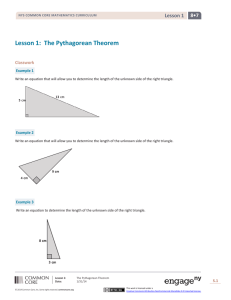
... MGSE9-12.F.IF.6 Calculate and interpret the average rate of change of a function (presented symbolically or as a table) over a specified interval. Estimate the rate of change from a graph. Analyze functions using different representations MGSE9-12.F.IF.7 Graph functions expressed algebraically and s ...
... MGSE9-12.F.IF.6 Calculate and interpret the average rate of change of a function (presented symbolically or as a table) over a specified interval. Estimate the rate of change from a graph. Analyze functions using different representations MGSE9-12.F.IF.7 Graph functions expressed algebraically and s ...
Unit 3 Introduction to Rational Number Class - VII - CBSE
... a continuous and comprehensive basis consequent to the mutual interactions between the teacher and the learner. There are some non-evaluative components in the curriculum which would be commented upon by the teachers and the school. The objective of this part or the core of the curriculum is to scaf ...
... a continuous and comprehensive basis consequent to the mutual interactions between the teacher and the learner. There are some non-evaluative components in the curriculum which would be commented upon by the teachers and the school. The objective of this part or the core of the curriculum is to scaf ...
Theories and uses of context in knowledge representation and
... Interestingly enough, KRR seems to share this intuition with other related areas. Two examples will illustrate this “family resemblance”. Sperber and Wilson, in their book on relevance (1986:15), express a similar intuition from a psycholinguistic perspective: “The set of premises used in interpreti ...
... Interestingly enough, KRR seems to share this intuition with other related areas. Two examples will illustrate this “family resemblance”. Sperber and Wilson, in their book on relevance (1986:15), express a similar intuition from a psycholinguistic perspective: “The set of premises used in interpreti ...
p-ADIC QUOTIENT SETS
... real numbers R+ has been examined by many authors over the years [3–7, 14, 20, 21, 24, 26, 27, 29, 32, 33, 36–38]. Analogues in the Gaussian integers [12] and, more generally, in imaginary quadratic number fields [34] have been considered. Since R(A) is a subset of the rational numbers Q, there are ...
... real numbers R+ has been examined by many authors over the years [3–7, 14, 20, 21, 24, 26, 27, 29, 32, 33, 36–38]. Analogues in the Gaussian integers [12] and, more generally, in imaginary quadratic number fields [34] have been considered. Since R(A) is a subset of the rational numbers Q, there are ...
lecture notes in logic - UCLA Department of Mathematics
... additional symbols which are common to all FOL(τ ). 1. The logical symbols ¬ & ∨ → ∀ ∃ = 2. The punctuation symbols ( ) , 3. The (individual) variables: v0 , v1 , v2 , . . . Here ¬ (not), & (and), ∨ (or) and → (implies) are the propositional symbols, and ∀ (for all) and ∃ (there exists) are the quan ...
... additional symbols which are common to all FOL(τ ). 1. The logical symbols ¬ & ∨ → ∀ ∃ = 2. The punctuation symbols ( ) , 3. The (individual) variables: v0 , v1 , v2 , . . . Here ¬ (not), & (and), ∨ (or) and → (implies) are the propositional symbols, and ∀ (for all) and ∃ (there exists) are the quan ...
Document
... To Teachers and Tutors: Below is a list of key words and phrases in this teach yourself unit. To Students: You can skip this list and begin your algebra exploration on the next page. After you have completed this unit, you will know much about the words and phrases in the list. Key words and phrases ...
... To Teachers and Tutors: Below is a list of key words and phrases in this teach yourself unit. To Students: You can skip this list and begin your algebra exploration on the next page. After you have completed this unit, you will know much about the words and phrases in the list. Key words and phrases ...