Interpretability formalized
... As with all sciences, mathematics aims at a better description and understanding of reality. Now, the logician asks: what is mathematical reality? Mathematics deals with numbers, functions, shapes, circles, sets, etc. But who has ever touched a number? Who has ever seen a real circle? The firm and u ...
... As with all sciences, mathematics aims at a better description and understanding of reality. Now, the logician asks: what is mathematical reality? Mathematics deals with numbers, functions, shapes, circles, sets, etc. But who has ever touched a number? Who has ever seen a real circle? The firm and u ...
Everything Else Being Equal: A Modal Logic for Ceteris Paribus
... The paper is organized as follows. In Section 2, we present and discuss von Wright’s original work in preference logic, in order to motivate some of the notions we develop later, but also as a foundational standard against which we can evaluate our own results. In Section 3, we present a basic modal ...
... The paper is organized as follows. In Section 2, we present and discuss von Wright’s original work in preference logic, in order to motivate some of the notions we develop later, but also as a foundational standard against which we can evaluate our own results. In Section 3, we present a basic modal ...
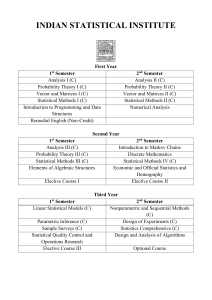
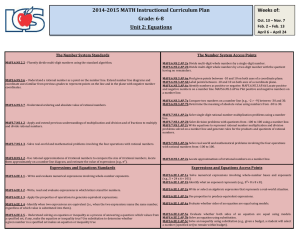
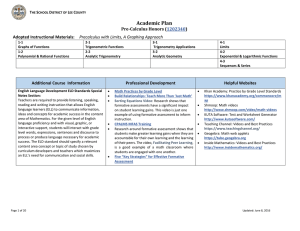
Document
... 4. The bleachers at a football game is 7/8 full, and half the fans are rooting for the home team. What fraction of the bleacher is rooting for the home team? ...
... 4. The bleachers at a football game is 7/8 full, and half the fans are rooting for the home team. What fraction of the bleacher is rooting for the home team? ...
1 Non-deterministic Phase Semantics and the Undecidability of
... directly into BBI and Kripke semantics, exactly as this was later done for Classical BI in [LarcheyWendling 2010]. But then, the intuition behind the encoding is arguably much more difficult to grasp. We also feel that the existence of the elementary fragment of ILL is important in itself, and in pa ...
... directly into BBI and Kripke semantics, exactly as this was later done for Classical BI in [LarcheyWendling 2010]. But then, the intuition behind the encoding is arguably much more difficult to grasp. We also feel that the existence of the elementary fragment of ILL is important in itself, and in pa ...
7-4 - Humble ISD
... Most calculators calculate logarithms only in base 10 or base e (see Lesson 7-6). You can change a logarithm in one base to a logarithm in another base with the following formula. ...
... Most calculators calculate logarithms only in base 10 or base e (see Lesson 7-6). You can change a logarithm in one base to a logarithm in another base with the following formula. ...
here
... Proposition 2. Assume the numbers r, s, and t are as in Lemma 1. If either (i). 16 6= r ∈ N, or (ii). rn ∈ Q \ Q for all n ∈ N, then at least one of the numbers s and t is transcendental. In [15, Conjecture 3.7] we made the following prediction. Conjecture 2. A stronger conclusion holds in Propositi ...
... Proposition 2. Assume the numbers r, s, and t are as in Lemma 1. If either (i). 16 6= r ∈ N, or (ii). rn ∈ Q \ Q for all n ∈ N, then at least one of the numbers s and t is transcendental. In [15, Conjecture 3.7] we made the following prediction. Conjecture 2. A stronger conclusion holds in Propositi ...