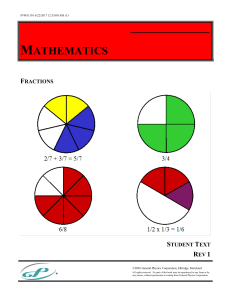
Reducing Fractions
... Whole numbers are used for counting; that is, describing the number of objects in a group. However, the result of a measurement need not be a whole number, and in fact, rarely is. The number of pages in this book is by definition a whole number, but the weight of the book in pounds is probably not a ...
... Whole numbers are used for counting; that is, describing the number of objects in a group. However, the result of a measurement need not be a whole number, and in fact, rarely is. The number of pages in this book is by definition a whole number, but the weight of the book in pounds is probably not a ...
a semantic perspective - Institute for Logic, Language and
... chapters in this handbook. Thus the reader will find here definitions and discussions of all the basic tools needed in modal model theory (such as the standard translation, generated submodels, bounded morphisms, and so on). Basic results about these concepts are stated and some simple proofs are gi ...
... chapters in this handbook. Thus the reader will find here definitions and discussions of all the basic tools needed in modal model theory (such as the standard translation, generated submodels, bounded morphisms, and so on). Basic results about these concepts are stated and some simple proofs are gi ...
Representing Numbers Using Fibonacci Variants
... fk is the closest natural number to φk / 5, the ratio of Fibonacci numbers approaches φ. Thus Zeckendorf representation has roughly base φ ≈ 1.618 < 2, less efficient than binary. But Zeckendorf representation can’t contain a pair of consecutive ones, so a pair can be used to separate numbers in a l ...
... fk is the closest natural number to φk / 5, the ratio of Fibonacci numbers approaches φ. Thus Zeckendorf representation has roughly base φ ≈ 1.618 < 2, less efficient than binary. But Zeckendorf representation can’t contain a pair of consecutive ones, so a pair can be used to separate numbers in a l ...
Mathematical Reasoning: Writing and Proof
... Students are introduced to a method to organize their thought processes when attempting to construct a proof that uses a so-called know-show table. (See Section 1.2 and Section 3.1.) Students use this table to work backward from what it is they are trying to prove while at the same time working forw ...
... Students are introduced to a method to organize their thought processes when attempting to construct a proof that uses a so-called know-show table. (See Section 1.2 and Section 3.1.) Students use this table to work backward from what it is they are trying to prove while at the same time working forw ...