CHAPTER 8 Hilbert Proof Systems, Formal Proofs, Deduction
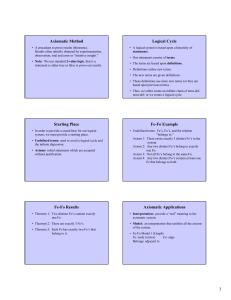
... possible to ”reverse” their use; to use them in the reverse manner in order to search for proofs, and we were able to do so in a blind, fully automatic way. We were able to conduct an argument of the type: if this formula has a proof the only way to construct it is from such and such formulas by th ...
... possible to ”reverse” their use; to use them in the reverse manner in order to search for proofs, and we were able to do so in a blind, fully automatic way. We were able to conduct an argument of the type: if this formula has a proof the only way to construct it is from such and such formulas by th ...
Total interval numbers of complete r
... each set of F as a vertex and joining two vertices with an edge if their corresponding sets intersect. The family of sets is called an intersection representation of its intersection graph. For an intersection representation F of a graph G = (V; E), we often use a bijection f from V to F to represen ...
... each set of F as a vertex and joining two vertices with an edge if their corresponding sets intersect. The family of sets is called an intersection representation of its intersection graph. For an intersection representation F of a graph G = (V; E), we often use a bijection f from V to F to represen ...
Second-Order Logic of Paradox
... This conjunction is true (though also, because of its universally quantified Second-order conjunct, also false: it takes the value Both) in Secondorder LP models with the genuine natural numbers as individuals and in many, though not all, of the finite inconsistent models described in Priest [12]: t ...
... This conjunction is true (though also, because of its universally quantified Second-order conjunct, also false: it takes the value Both) in Secondorder LP models with the genuine natural numbers as individuals and in many, though not all, of the finite inconsistent models described in Priest [12]: t ...
Q. 1 – Q. 5 carry one mark each.
... ming numberr of people innfected with h rabies in Inndia has beenn flagged by y the World Heaalth Organizzation as a soource of conncern. It is esstimated thatt inoculatingg 70% of petts and stray doggs against rabbies can leadd to a significcant reductio on in the num mber of peoplle infected with ...
... ming numberr of people innfected with h rabies in Inndia has beenn flagged by y the World Heaalth Organizzation as a soource of conncern. It is esstimated thatt inoculatingg 70% of petts and stray doggs against rabbies can leadd to a significcant reductio on in the num mber of peoplle infected with ...