Proof Theory in Type Theory
... notion of ordinals is not enough to represent the closure ordinal of the classical version of B. The definition of ordinals use the notion of function, which is quite different intuitionistically and classically. May be the need of an extension of (S0 ) comes from this difference. Another question i ...
... notion of ordinals is not enough to represent the closure ordinal of the classical version of B. The definition of ordinals use the notion of function, which is quite different intuitionistically and classically. May be the need of an extension of (S0 ) comes from this difference. Another question i ...
Chapter 11 Review JEOPARDY
... Distinguish between relations that are functions and those that are not functions Recognize functions in a variety of representations and a variety of contexts Uses tables to describe sequences recursively and with a formula in closed form Understand and recognize arithmetic sequences as linear func ...
... Distinguish between relations that are functions and those that are not functions Recognize functions in a variety of representations and a variety of contexts Uses tables to describe sequences recursively and with a formula in closed form Understand and recognize arithmetic sequences as linear func ...
Quotients of Fibonacci Numbers
... endowed with metrics other than the one inherited from R. For each prime p, there is a p-adic metric on Q, with respect to which Q can be completed to form the set Q p of p-adic numbers. Our aim here is to prove the following theorem. Theorem 2. R(F) is dense in Q p for every prime p. By this we mea ...
... endowed with metrics other than the one inherited from R. For each prime p, there is a p-adic metric on Q, with respect to which Q can be completed to form the set Q p of p-adic numbers. Our aim here is to prove the following theorem. Theorem 2. R(F) is dense in Q p for every prime p. By this we mea ...
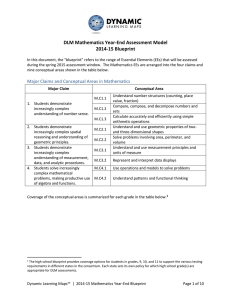
CCMath8unit2parentletter[1]
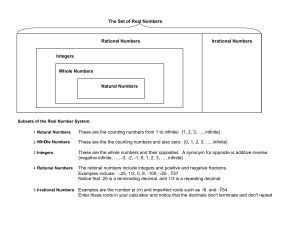
... Scientific Notation (Exponential Notation): A representation of real numbers as the product of a number between 1 and 10 and a power of 10, used primarily for very large or very small numbers. Square root: One of two equal factors of a nonnegative number. For example, 5 is a square root of 25 becaus ...
... Scientific Notation (Exponential Notation): A representation of real numbers as the product of a number between 1 and 10 and a power of 10, used primarily for very large or very small numbers. Square root: One of two equal factors of a nonnegative number. For example, 5 is a square root of 25 becaus ...
Full text
... In the study of a combinatorial minimization problem related to multimodule computer memory organizations [ 5 ] , a triangle of numbers is constructed, which enjoys many of the pleasant properties of Pascal's triangle [1,2]. These numbers originate from counting a set of points in the /r-dimensional ...
... In the study of a combinatorial minimization problem related to multimodule computer memory organizations [ 5 ] , a triangle of numbers is constructed, which enjoys many of the pleasant properties of Pascal's triangle [1,2]. These numbers originate from counting a set of points in the /r-dimensional ...
order of operations
... • Begin your own mathematics “dictionary” • Include all new terms, a definition, and an example for each term • You will find it invaluable as we progress from unit to unit! ...
... • Begin your own mathematics “dictionary” • Include all new terms, a definition, and an example for each term • You will find it invaluable as we progress from unit to unit! ...
01-NumberTheoryslides
... • Finds primes up to n from knowledge of primes up to n • Easy to implement in a graphical form ...
... • Finds primes up to n from knowledge of primes up to n • Easy to implement in a graphical form ...







![CCMath8unit2parentletter[1]](http://s1.studyres.com/store/data/009217078_1-e43411c7321cd6ee4502e10414c3d4f8-300x300.png)