MAA245 NUMBERS 1 Natural Numbers, N
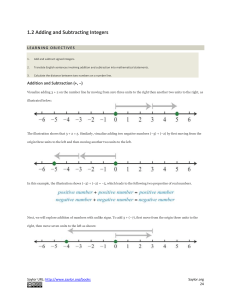
... convenient, we can denote the positive integer Ks = {(k + s, k); k ∈ N} by s. Also, denote the negative integer Lt = {(k, k + t), t ∈ N} by −t. Using ordered-pair arithmetic (i.e. (1) and (2)), and applying properties of N to each member of an ordered pair, we can show that + and × on Z have similar ...
... convenient, we can denote the positive integer Ks = {(k + s, k); k ∈ N} by s. Also, denote the negative integer Lt = {(k, k + t), t ∈ N} by −t. Using ordered-pair arithmetic (i.e. (1) and (2)), and applying properties of N to each member of an ordered pair, we can show that + and × on Z have similar ...
Binary Numbers – The Computer Number System • Number systems
... Binary digIT, or bit. Computers perform operations on binary number groups called words. Computer numbers are 1 and 0! Today, most computers use 32- or 64A simple electronic switch can represent bit words: – Words are subdivided into 8-bit both binary computer numbers groups called bytes. – One-half ...
... Binary digIT, or bit. Computers perform operations on binary number groups called words. Computer numbers are 1 and 0! Today, most computers use 32- or 64A simple electronic switch can represent bit words: – Words are subdivided into 8-bit both binary computer numbers groups called bytes. – One-half ...
Polynomial Packet Notes - Magoffin County Schools
... • simplify special products in more challenging problems that I have never previously attempted I am able to • find the square of a binomial • find the product of a sum and difference I am able to • find the square of a binomial with help • find the product of a sum and difference with help I am abl ...
... • simplify special products in more challenging problems that I have never previously attempted I am able to • find the square of a binomial • find the product of a sum and difference I am able to • find the square of a binomial with help • find the product of a sum and difference with help I am abl ...
Part 1: Introduction
... significant digits and the m least significant digits These are called fixed-point representations Programmer not restricted to the predetermined position of the radix point Operands can be scaled - same scaling for all operands Add and subtract operations are correct aX aY=a(X Y) (a - ...
... significant digits and the m least significant digits These are called fixed-point representations Programmer not restricted to the predetermined position of the radix point Operands can be scaled - same scaling for all operands Add and subtract operations are correct aX aY=a(X Y) (a - ...
Uncertainty in Measurements & Significant Figures
... scientific data and report the results of calculations. What is special about significant figures is that in a decimal number, only the last integer is presumed to be estimated. In other words, the number of significant figures allows you to communicate how certain the value is that is being reporte ...
... scientific data and report the results of calculations. What is special about significant figures is that in a decimal number, only the last integer is presumed to be estimated. In other words, the number of significant figures allows you to communicate how certain the value is that is being reporte ...
Compare And Order Non-rational numbers - Math GR. 6-8
... Benchmark MA.6.A.5.3 Estimate the results of computations with fractions, decimals, and percents and judge the reasonableness of the results ...
... Benchmark MA.6.A.5.3 Estimate the results of computations with fractions, decimals, and percents and judge the reasonableness of the results ...
Arithmetic

Arithmetic or arithmetics (from the Greek ἀριθμός arithmos, ""number"") is the oldest and most elementary branch of mathematics. It consists of the study of numbers, especially the properties of the traditional operations between them—addition, subtraction, multiplication and division. Arithmetic is an elementary part of number theory, and number theory is considered to be one of the top-level divisions of modern mathematics, along with algebra, geometry, and analysis. The terms arithmetic and higher arithmetic were used until the beginning of the 20th century as synonyms for number theory and are sometimes still used to refer to a wider part of number theory.