multiply
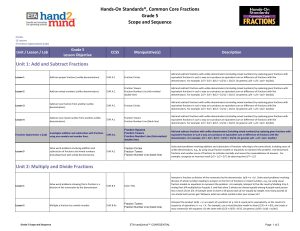
... use the order of operation to simplify numerical expression containing rational numbers ...
... use the order of operation to simplify numerical expression containing rational numbers ...
Multiplying Fractions
... An integer can be considered to be a fraction with a denominator of 1. Therefore when a fraction is multiplied by an integer the numerator of the fraction is multiplied by the integer. The denominator is multiplied by 1 which does not change the denominator. (simplify if necessary) Multiplying Mixed ...
... An integer can be considered to be a fraction with a denominator of 1. Therefore when a fraction is multiplied by an integer the numerator of the fraction is multiplied by the integer. The denominator is multiplied by 1 which does not change the denominator. (simplify if necessary) Multiplying Mixed ...
HOSCCFractions_G3_G4_G5_SS_11 12 13
... Add and subtract fractions with unlike denominators (including mixed numbers) by replacing given fractions with equivalent fractions in such a way as to produce an equivalent sum or difference of fractions with like denominators. For example, 2/3 + 5/4 = 8/12 + 15/12 = 23/12. (In general, a/b + c/ ...
... Add and subtract fractions with unlike denominators (including mixed numbers) by replacing given fractions with equivalent fractions in such a way as to produce an equivalent sum or difference of fractions with like denominators. For example, 2/3 + 5/4 = 8/12 + 15/12 = 23/12. (In general, a/b + c/ ...
all positive integers are polite numbers except powers
... contradiction is reached. But this might not answer any other questions about what forms these representations take. Looking at a table of representations, it is clear that some numbers have lots of representation, and that there are patterns to these representations. Proving this theorem, however, ...
... contradiction is reached. But this might not answer any other questions about what forms these representations take. Looking at a table of representations, it is clear that some numbers have lots of representation, and that there are patterns to these representations. Proving this theorem, however, ...
Arithmetic

Arithmetic or arithmetics (from the Greek ἀριθμός arithmos, ""number"") is the oldest and most elementary branch of mathematics. It consists of the study of numbers, especially the properties of the traditional operations between them—addition, subtraction, multiplication and division. Arithmetic is an elementary part of number theory, and number theory is considered to be one of the top-level divisions of modern mathematics, along with algebra, geometry, and analysis. The terms arithmetic and higher arithmetic were used until the beginning of the 20th century as synonyms for number theory and are sometimes still used to refer to a wider part of number theory.