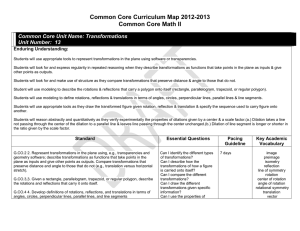
STEP Support Programme Assignment 9 Warm-up
... propositions each one relying only on previous propositions. Euclid’s Elements were used as a basis for teaching geometry for 23 centuries. The logical structure of Euclid’s Elements is the model for the teaching of other subjects, notably university level mathematical analysis which lays the founda ...
... propositions each one relying only on previous propositions. Euclid’s Elements were used as a basis for teaching geometry for 23 centuries. The logical structure of Euclid’s Elements is the model for the teaching of other subjects, notably university level mathematical analysis which lays the founda ...
Cornell notes
... CONSECUTIVE INTERIOR ANGLES THEOREM • Two lines cut by a transversal are parallel if and only if the pairs of consecutive interior angles are supplementary. ...
... CONSECUTIVE INTERIOR ANGLES THEOREM • Two lines cut by a transversal are parallel if and only if the pairs of consecutive interior angles are supplementary. ...
isosceles triangles
... In geometry, the centroid, geometric center, or barycenter of a plane figure is the intersection of all straight lines that divide the figure into two parts of equal moment about the line. ...
... In geometry, the centroid, geometric center, or barycenter of a plane figure is the intersection of all straight lines that divide the figure into two parts of equal moment about the line. ...