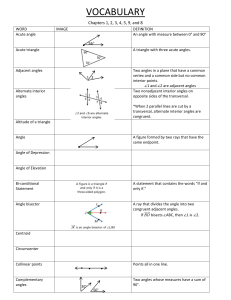
Section 9.1
... Two lines in a plane can be either parallel or intersecting. Parallel lines never meet. Intersecting lines meet at a point. The symbol is used to denote “is parallel to.” ...
... Two lines in a plane can be either parallel or intersecting. Parallel lines never meet. Intersecting lines meet at a point. The symbol is used to denote “is parallel to.” ...