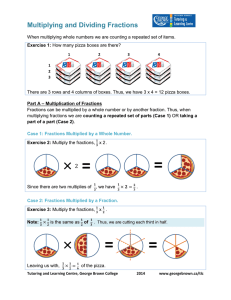
Estimate Quotients Using Multiples
... Division and the Distributive Property Divide. 78 4 6 Use the Distributive Property and quick pictures to break apart numbers to make them easier to divide. Step 1 Draw a quick picture to show 78. Step 2 Think about how to break apart 78. You know 6 tens 4 6 5 10, so use 78 5 60 1 18. Draw a quick ...
... Division and the Distributive Property Divide. 78 4 6 Use the Distributive Property and quick pictures to break apart numbers to make them easier to divide. Step 1 Draw a quick picture to show 78. Step 2 Think about how to break apart 78. You know 6 tens 4 6 5 10, so use 78 5 60 1 18. Draw a quick ...
fractions
... Denominator: the bottom number and shows how many equal parts there are in all. Whole Number: a number with no fractional (or left over) parts. A whole number is also called an integer. All whole numbers can be expressed as a fraction with that number over 1. For example: the whole number 8 = 8/1, t ...
... Denominator: the bottom number and shows how many equal parts there are in all. Whole Number: a number with no fractional (or left over) parts. A whole number is also called an integer. All whole numbers can be expressed as a fraction with that number over 1. For example: the whole number 8 = 8/1, t ...
Fractions IV Equivalent Fractions
... a dollar, which has 100 pennies and divide it by the denominator (which is 4), then we would end up with 25. That’s 25 pennies! ...
... a dollar, which has 100 pennies and divide it by the denominator (which is 4), then we would end up with 25. That’s 25 pennies! ...
GRE Math Review 1 Arithmetic
... itself. The first ten prime numbers are 2, 3, 5, 7, 11, 13, 17, 19, 23, and 29. The integer 14 is not a prime number, since it has four positive divisors: 1, 2, 7, and 14. The integer 1 is not a prime number, and the integer 2 is the only prime number that is even. ...
... itself. The first ten prime numbers are 2, 3, 5, 7, 11, 13, 17, 19, 23, and 29. The integer 14 is not a prime number, since it has four positive divisors: 1, 2, 7, and 14. The integer 1 is not a prime number, and the integer 2 is the only prime number that is even. ...
A. Multiplying Two 2-digit Numbers: 47 x 38
... then the entire original number will be divisible by 11. This means we need to find a digit n, such that n – 3 is equal to 11, 22, 33, etc, and don’t forget 0!! If n = 3, then n – 3 = 0 which is divisible by 11. ...
... then the entire original number will be divisible by 11. This means we need to find a digit n, such that n – 3 is equal to 11, 22, 33, etc, and don’t forget 0!! If n = 3, then n – 3 = 0 which is divisible by 11. ...
Full text
... In [ 2 ] , it was shown how to obtain the coordinates of a point in (real) three-dimensional Euclidean space as triple products of Fibonacci numbers. This was achieved as a development of two-dimensional ideas involving complex numbers, though the three-dimensional extension was devoid of any depend ...
... In [ 2 ] , it was shown how to obtain the coordinates of a point in (real) three-dimensional Euclidean space as triple products of Fibonacci numbers. This was achieved as a development of two-dimensional ideas involving complex numbers, though the three-dimensional extension was devoid of any depend ...
S F L
... The least common multiple (LCM) of a given set of numbers is the smallest positive number divisible by the numbers in the set. For example, if we list the multiples of 4 and 6, we can see these numbers share common multiples of 12, 24, 36, and 48 to name a few. Multiples of 4: 4, 8, 12, 16, 20, 24, ...
... The least common multiple (LCM) of a given set of numbers is the smallest positive number divisible by the numbers in the set. For example, if we list the multiples of 4 and 6, we can see these numbers share common multiples of 12, 24, 36, and 48 to name a few. Multiples of 4: 4, 8, 12, 16, 20, 24, ...
Multiplication and Division
... Pupils develop efficient mental methods, for example, using commutativity and associativity (for example, 4 × 12 × 5 = 4 × 5 × 12 = 20 × 12 = 240) and multiplication and division facts (for example, using 3 × 2 = 6, 6 ÷ 3 = 2 and 2 = 6 ÷ 3) to derive related facts (for example, 30 × 2 = 60, 60 ÷ 3 = ...
... Pupils develop efficient mental methods, for example, using commutativity and associativity (for example, 4 × 12 × 5 = 4 × 5 × 12 = 20 × 12 = 240) and multiplication and division facts (for example, using 3 × 2 = 6, 6 ÷ 3 = 2 and 2 = 6 ÷ 3) to derive related facts (for example, 30 × 2 = 60, 60 ÷ 3 = ...