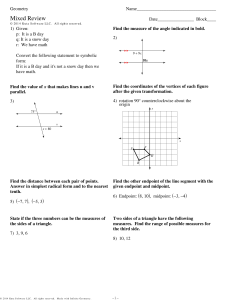
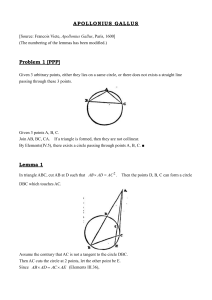
Lesson 13: The Inscribed Angle Alternate a Tangent
... their segment and angle relationships. Bring the class back together and share, allowing students to add to their list. ...
... their segment and angle relationships. Bring the class back together and share, allowing students to add to their list. ...
SSLC - MATHEMATICS CHAPTER 10 CIRCLES ENGLISH VERSION
... SSLC CLASS NOTES: CHAPTER 10-CIRCLES [English Version] 4. In the given quadrilateral ABCD,BC = 38cm, QB = 27cm, DC = 25cm and AD⟘DC find the radius of the circle . In the figure OPDS , DS = DP [∵tangents drawn from an external point] OP = OS [∵ Radius of a circle] ∠D = 900 [∵AD⟘DC] ∴ OPDS is a squar ...
... SSLC CLASS NOTES: CHAPTER 10-CIRCLES [English Version] 4. In the given quadrilateral ABCD,BC = 38cm, QB = 27cm, DC = 25cm and AD⟘DC find the radius of the circle . In the figure OPDS , DS = DP [∵tangents drawn from an external point] OP = OS [∵ Radius of a circle] ∠D = 900 [∵AD⟘DC] ∴ OPDS is a squar ...
Segments of Circles: Theorems for secants and
... 2. As a class, prove the following three theorems using similar and congruent triangles i. If two tangent segments are drawn to a circle from an external point, then both tangent segments are congruent. ii. If a tangent segment and a secant segment are drawn to a circle from an exterior point, then ...
... 2. As a class, prove the following three theorems using similar and congruent triangles i. If two tangent segments are drawn to a circle from an external point, then both tangent segments are congruent. ii. If a tangent segment and a secant segment are drawn to a circle from an exterior point, then ...
ΔFEG is not a right triangle, so is not tangent to circle E.
... . (Through a point not on a line exactly one perpendicular can be drawn to another line.) Since ∠STP is a right angle, PQST is a rectangle with PT = QS or 4 and PQ = ST. Triangle RST is a right triangle with RT = PR – TR or 2 and RS = PR + QS or 10. Let x = TS and use the Pythagorean Theorem to fin ...
... . (Through a point not on a line exactly one perpendicular can be drawn to another line.) Since ∠STP is a right angle, PQST is a rectangle with PT = QS or 4 and PQ = ST. Triangle RST is a right triangle with RT = PR – TR or 2 and RS = PR + QS or 10. Let x = TS and use the Pythagorean Theorem to fin ...
lesson plan 12-8
... Day & Date: Monday, December 8, 2014 Standard: MCC9-12.G.C.2 Identify and describe relationships among inscribed angles, radii, and chords. Include the relationship between central, inscribed, and circumscribed angles; inscribed angles on a diameter are right angles; the radius of a circle is perpen ...
... Day & Date: Monday, December 8, 2014 Standard: MCC9-12.G.C.2 Identify and describe relationships among inscribed angles, radii, and chords. Include the relationship between central, inscribed, and circumscribed angles; inscribed angles on a diameter are right angles; the radius of a circle is perpen ...
Circles, Part 2 - Providence Public Schools
... students’ understanding of the big ideas indicated within the standards. The CCSS for Mathematical Content and the CCSS for Mathematical Practice should be considered when designing assessments. Standards-based mathematics assessment items should vary in difficulty, content, and type. The assessment ...
... students’ understanding of the big ideas indicated within the standards. The CCSS for Mathematical Content and the CCSS for Mathematical Practice should be considered when designing assessments. Standards-based mathematics assessment items should vary in difficulty, content, and type. The assessment ...
Geometry Lesson Plan Unit: 10 Circles Lesson Topic(s): Parts of a
... → Arc addition postulate of adjacent arcs is the sum of their measures →Two minor arcs are congruent if and only if their corresponding arcs are congruent →The diameter of a circle is perpendicular to a chord then the diameter bisects the chord and the arc →If one chord is perpendicular bisector of ...
... → Arc addition postulate of adjacent arcs is the sum of their measures →Two minor arcs are congruent if and only if their corresponding arcs are congruent →The diameter of a circle is perpendicular to a chord then the diameter bisects the chord and the arc →If one chord is perpendicular bisector of ...
High School Math 3 Unit 5: Circles
... similar. In Math 1 and earlier in Math 2, students used the logical structure behind conditional statements to prove various relationships between geometric objects. The properties of congruent and similar triangles have been used in proofs. In Grade 8, students applied the Pythagorean Theorem to fi ...
... similar. In Math 1 and earlier in Math 2, students used the logical structure behind conditional statements to prove various relationships between geometric objects. The properties of congruent and similar triangles have been used in proofs. In Grade 8, students applied the Pythagorean Theorem to fi ...
Mathematics Methods Investigations
... The ability to prove two triangles are congruent is assumed together with the knowledge of the exterior angle of a triangle theorem, the central angle theorem and the angle in the alternate segment theorem. It is also assumed that students are familiar with the method of proof by contradiction (Spec ...
... The ability to prove two triangles are congruent is assumed together with the knowledge of the exterior angle of a triangle theorem, the central angle theorem and the angle in the alternate segment theorem. It is also assumed that students are familiar with the method of proof by contradiction (Spec ...
Unit 2
... Understand angle sum and exterior angle of triangles. Know facts about supplementary, complementary, vertical, and adjacent angles. Solve problems involving scale drawings of geometric figures. Draw geometric shapes with given conditions. Draw polygons in the coordinate plane given coordinates for t ...
... Understand angle sum and exterior angle of triangles. Know facts about supplementary, complementary, vertical, and adjacent angles. Solve problems involving scale drawings of geometric figures. Draw geometric shapes with given conditions. Draw polygons in the coordinate plane given coordinates for t ...
Tangent lines to circles
In Euclidean plane geometry, a tangent line to a circle is a line that touches the circle at exactly one point, never entering the circle's interior. Roughly speaking, it is a line through a pair of infinitely close points on the circle. Tangent lines to circles form the subject of several theorems, and play an important role in many geometrical constructions and proofs. Since the tangent line to a circle at a point P is perpendicular to the radius to that point, theorems involving tangent lines often involve radial lines and orthogonal circles.