Spatial Randomness
... where is again the expected point density (i.e., expected number of points per unit area). To see this, note simply that the basic Laplace argument in Figure 1.1 of Section 1 depends only on similarities among individual cells in uniform grids of cells. But since such cells are all translations of ...
... where is again the expected point density (i.e., expected number of points per unit area). To see this, note simply that the basic Laplace argument in Figure 1.1 of Section 1 depends only on similarities among individual cells in uniform grids of cells. But since such cells are all translations of ...
6.1A Notes File - Northwest ISD Moodle
... A numerical variable that describes the outcomes of a chance process (like X in the coin-tossing scenario) is called a random variable. The probability model for a random variable is its probability distribution. A random variable takes numerical values that describe the outcomes of some chance proc ...
... A numerical variable that describes the outcomes of a chance process (like X in the coin-tossing scenario) is called a random variable. The probability model for a random variable is its probability distribution. A random variable takes numerical values that describe the outcomes of some chance proc ...
Notes for Lesson 10-7: Independent and Dependent Events
... the probability of the other event Dependent Events – Events for which the occurrence or non-occurrence of one event affects the probability of the other event When one outcome depends on outcome of another event, or when one event affects the probability of the other then the two events are connect ...
... the probability of the other event Dependent Events – Events for which the occurrence or non-occurrence of one event affects the probability of the other event When one outcome depends on outcome of another event, or when one event affects the probability of the other then the two events are connect ...
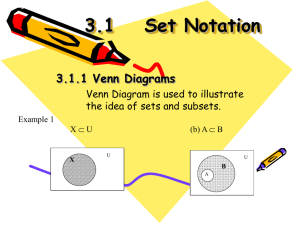
3.1 Set Notation
... – In how many ways can a hand of 4 cards be dealt from an ordinary pack of 52 palying cards? ...
... – In how many ways can a hand of 4 cards be dealt from an ordinary pack of 52 palying cards? ...
Lesson 12-8
... then the two events are connected to each other and are said to be Dependent Events. If two event that happen at the same time do not affect the probability of each other then the two events are Independent of each other. A dime lands heads up and a nickel lands heads up – Independent You choose a g ...
... then the two events are connected to each other and are said to be Dependent Events. If two event that happen at the same time do not affect the probability of each other then the two events are Independent of each other. A dime lands heads up and a nickel lands heads up – Independent You choose a g ...
Math 115
... 11) A coin is tossed five times. Find the probability of getting at least 1 tail. P(at least 1 tail) = 1 – P(no tails) = 1 - ...
... 11) A coin is tossed five times. Find the probability of getting at least 1 tail. P(at least 1 tail) = 1 – P(no tails) = 1 - ...
Probability Quiz
... A coin is biased in such a way that in the long run, on the average, a head turns up 3 times in 10 tosses. If this biased coin is tossed simultaneously with an unbiased coin, what is the probability that both will fall as heads? ...
... A coin is biased in such a way that in the long run, on the average, a head turns up 3 times in 10 tosses. If this biased coin is tossed simultaneously with an unbiased coin, what is the probability that both will fall as heads? ...
5.1.1 The Idea of Probability Chance behavior is unpredictable in
... How do insurance companies decide how much to charge for life insurance? We can’t predict whether a particular person will die in the next year. But the National Center for Health Statistics says that ...
... How do insurance companies decide how much to charge for life insurance? We can’t predict whether a particular person will die in the next year. But the National Center for Health Statistics says that ...
recommendedBooks
... Nate Silver, The Signal and the Noise: Why So Many Predictions Fail – but Some Don’t, Penguin Press (2012) Nassim Nicholas Taleb, The Black Swan: The Impact of the Highly Improbable, 2nd edition, Random House (2010) http://www.wimp.com/hilarious-probability/ Bangkok insurance ...
... Nate Silver, The Signal and the Noise: Why So Many Predictions Fail – but Some Don’t, Penguin Press (2012) Nassim Nicholas Taleb, The Black Swan: The Impact of the Highly Improbable, 2nd edition, Random House (2010) http://www.wimp.com/hilarious-probability/ Bangkok insurance ...
Set Prob 7 - Non-Mutually Exclusive
... a) Are skipping breakfast and skipping lunch mutually exclusive events? Explain. ...
... a) Are skipping breakfast and skipping lunch mutually exclusive events? Explain. ...
PLEASE read this (exam notice)!
... b. What is the minimum possible value for P(AB)? c. What is the maximum possible value for P(ABc)? d. What is the minimum possible value for P(ABc)? ...
... b. What is the minimum possible value for P(AB)? c. What is the maximum possible value for P(ABc)? d. What is the minimum possible value for P(ABc)? ...
Notes on Probability
... members of ecn 215 being present in class is .8 (let us say). What is the probability of both these events occurring? ...
... members of ecn 215 being present in class is .8 (let us say). What is the probability of both these events occurring? ...
continuous random variable
... each day you note the closing price of the stock. The result each day is a real number X (the closing price of the stock) in the unbounded interval [0, + infinity). OR ...
... each day you note the closing price of the stock. The result each day is a real number X (the closing price of the stock) in the unbounded interval [0, + infinity). OR ...
PDF
... You can reuse this document or portions thereof only if you do so under terms that are compatible with the CC-BY-SA license. ...
... You can reuse this document or portions thereof only if you do so under terms that are compatible with the CC-BY-SA license. ...
Form groups of two or three and discuss the following questions
... (iii) The outcome is expected to happen about two times out of every 100 trials. (iv) The outcome could happen, or it couldn't, the chances of either result are the same. (b) The Hai Meteorological Center wanted to determine the accuracy of their weather forecasts. They searched their records for th ...
... (iii) The outcome is expected to happen about two times out of every 100 trials. (iv) The outcome could happen, or it couldn't, the chances of either result are the same. (b) The Hai Meteorological Center wanted to determine the accuracy of their weather forecasts. They searched their records for th ...
TSG 14 Teaching and learning of probability - ICME-13
... again, re-formulate a research agenda in this area for the coming years. The group welcomes theoretical analyses and empirical research in probability education using a variety of research methods, coming from researchers and teachers that deal with any of the following topics: The nature of chanc ...
... again, re-formulate a research agenda in this area for the coming years. The group welcomes theoretical analyses and empirical research in probability education using a variety of research methods, coming from researchers and teachers that deal with any of the following topics: The nature of chanc ...
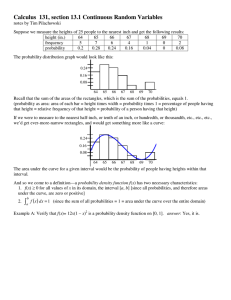
Calculus 131, section 13.1 Continuous Random Variables
... Recall that the sum of the areas of the rectangles, which is the sum of the probabilities, equals 1. (probability as area: area of each bar = height times width = probability times 1 = percentage of people having that height = relative frequency of that height = probability of a person having that h ...
... Recall that the sum of the areas of the rectangles, which is the sum of the probabilities, equals 1. (probability as area: area of each bar = height times width = probability times 1 = percentage of people having that height = relative frequency of that height = probability of a person having that h ...
`USING PROBABILITY TO DESCRIBE SITUATIONS`
... A card is drawn from a deck of 52 playing cards. Find the probability that it will be: a) the king of hearts b) a queen c) an ace, king, queen or jack d) the jack of spades or the ace of diamonds ...
... A card is drawn from a deck of 52 playing cards. Find the probability that it will be: a) the king of hearts b) a queen c) an ace, king, queen or jack d) the jack of spades or the ace of diamonds ...
Math 1312 – test II – Review
... different problems on the board ( one per student ). A student may or may not know the solution to a particular problem so it will matter whether the student is picked first, second , or third. How many different selections are possible ? ...
... different problems on the board ( one per student ). A student may or may not know the solution to a particular problem so it will matter whether the student is picked first, second , or third. How many different selections are possible ? ...
Unit 10
... When making judgments about probability, what must be true about the probability if one were to support an alternative hypothesis? ...
... When making judgments about probability, what must be true about the probability if one were to support an alternative hypothesis? ...
Computing Probabilities: Right Ways and Wrong Ways
... the X or the Y chromosome? Did you inherit grandma’s big nose? And on a more profound level, quantum physicists teach us that everything is governed by the laws of probability. They toss around terms like the Schrödinger wave equation and Heisenberg’s uncertainty principle, which are much too diffi ...
... the X or the Y chromosome? Did you inherit grandma’s big nose? And on a more profound level, quantum physicists teach us that everything is governed by the laws of probability. They toss around terms like the Schrödinger wave equation and Heisenberg’s uncertainty principle, which are much too diffi ...
6.16 independent and dependent practice
... spins a spinner with the letters M, O, N, E, and Y. What is the probability that the spinner will stop on the letter N on the first spin and an O the second spin? ...
... spins a spinner with the letters M, O, N, E, and Y. What is the probability that the spinner will stop on the letter N on the first spin and an O the second spin? ...
Sec. 6.3 Part 2 Blank Notes
... The multiplication rule says that the probability of reaching the end of any complete branch is the product of the probabilities written on its segments. ...
... The multiplication rule says that the probability of reaching the end of any complete branch is the product of the probabilities written on its segments. ...
Conditional probability and independence Bernoulli trials and the
... Independence of more than two events: Surprisingly, there are situations in which three or more events are independent of each other in pairs but are not independent of one another more generally. See the bottom of page 24 for an example. Events A1 , A2 , A3 , ... are independent if and only if the ...
... Independence of more than two events: Surprisingly, there are situations in which three or more events are independent of each other in pairs but are not independent of one another more generally. See the bottom of page 24 for an example. Events A1 , A2 , A3 , ... are independent if and only if the ...
History of randomness

In ancient history, the concepts of chance and randomness were intertwined with that of fate. Many ancient peoples threw dice to determine fate, and this later evolved into games of chance. At the same time, most ancient cultures used various methods of divination to attempt to circumvent randomness and fate.The Chinese were perhaps the earliest people to formalize odds and chance 3,000 years ago. The Greek philosophers discussed randomness at length, but only in non-quantitative forms. It was only in the sixteenth century that Italian mathematicians began to formalize the odds associated with various games of chance. The invention of modern calculus had a positive impact on the formal study of randomness. In the 19th century the concept of entropy was introduced in physics.The early part of the twentieth century saw a rapid growth in the formal analysis of randomness, and mathematical foundations for probability were introduced, leading to its axiomatization in 1933. At the same time, the advent of quantum mechanics changed the scientific perspective on determinacy. In the mid to late 20th-century, ideas of algorithmic information theory introduced new dimensions to the field via the concept of algorithmic randomness.Although randomness had often been viewed as an obstacle and a nuisance for many centuries, in the twentieth century computer scientists began to realize that the deliberate introduction of randomness into computations can be an effective tool for designing better algorithms. In some cases, such randomized algorithms are able to outperform the best deterministic methods.