Conservation of Energy Due to the fact that in a nonviscous flow
... To apply Bernoulli’s Theorem on a irrotational flow, one can take an exact first integral of the Euler’s Equation. However, the following restrictions have to be made: 1. The motion is irrotational, (where v is velocity field) 2. The external force is conservative, (where U is potential energy/unit ...
... To apply Bernoulli’s Theorem on a irrotational flow, one can take an exact first integral of the Euler’s Equation. However, the following restrictions have to be made: 1. The motion is irrotational, (where v is velocity field) 2. The external force is conservative, (where U is potential energy/unit ...
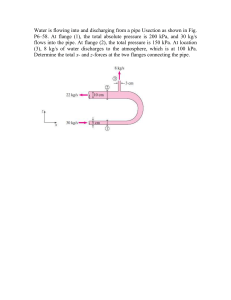
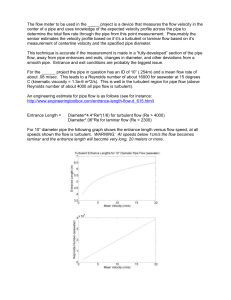
Water is flowing into and discharging from a pipe Usection as shown
... and gas absorption experiments. There is no applied pressure other than hydrostatic pressure due to gravity. Use the equations of motion in rectangular coordinates to derive expressions for: a) The velocity profile b) The pressure drop between the inlet and the exit points c) The total volumetric fl ...
... and gas absorption experiments. There is no applied pressure other than hydrostatic pressure due to gravity. Use the equations of motion in rectangular coordinates to derive expressions for: a) The velocity profile b) The pressure drop between the inlet and the exit points c) The total volumetric fl ...
AE 2350 Lecture Notes #5
... or if some external force is applied. – Example: A child squeezing a balloon ...
... or if some external force is applied. – Example: A child squeezing a balloon ...
UNDERVISNING I TPM VED HiB
... r = Fluid Density [kg/m3] V = Fluid Velocity [m/s] g = Gravitational Acceleration Constant [m/s2] h = Pressure Height or Submergence [m] ...
... r = Fluid Density [kg/m3] V = Fluid Velocity [m/s] g = Gravitational Acceleration Constant [m/s2] h = Pressure Height or Submergence [m] ...
Chapter 7b Specific head_Critical Depth_Hydraulic Jump b
... Let’s take the simple example of a rectangular channel, and then define q = Q/width. The area for a rectangle is A = base x height, so only the height part is left after we divide by the width ...
... Let’s take the simple example of a rectangular channel, and then define q = Q/width. The area for a rectangle is A = base x height, so only the height part is left after we divide by the width ...
Water Movement
... • Viscosity: resistance of a liquid to change of form. • Inertia: resistance of an object (body) to a change in its state of motion. • These two forces together influences an organism’s ability to move in water and how water flows. • The ratio of inertial force to viscous force is Re. ...
... • Viscosity: resistance of a liquid to change of form. • Inertia: resistance of an object (body) to a change in its state of motion. • These two forces together influences an organism’s ability to move in water and how water flows. • The ratio of inertial force to viscous force is Re. ...
Types of Flow
... particles get together and form a flowing stream. These particles, while moving, group themselves in a variety of ways, e.g., they move in a regular formation, just as disciplined soldiers do; or they may swirl, like the individuals, in a disorderly crowd. The type of flow of a liquid depends upon t ...
... particles get together and form a flowing stream. These particles, while moving, group themselves in a variety of ways, e.g., they move in a regular formation, just as disciplined soldiers do; or they may swirl, like the individuals, in a disorderly crowd. The type of flow of a liquid depends upon t ...
derived along a fluid flow streamline is often called the
... the Bernoulli family. He is particularly remembered for his applications of mathematics to mechanics, especially fluid mechanics, and for his pioneering work in probability and statistics. Bernoulli's work is still studied at length by many schools of science throughout the world. ...
... the Bernoulli family. He is particularly remembered for his applications of mathematics to mechanics, especially fluid mechanics, and for his pioneering work in probability and statistics. Bernoulli's work is still studied at length by many schools of science throughout the world. ...
Characteristics Method applied to the shock tube problem
... section of the tube, this pressure will limit the expansion wave to a narrower fan as sketched. The solution can be extended to the case where the ”right” fluid is also in motion. This then provides a numerical method called Godunov method introduced later on. The diaphragm represents the interface ...
... section of the tube, this pressure will limit the expansion wave to a narrower fan as sketched. The solution can be extended to the case where the ”right” fluid is also in motion. This then provides a numerical method called Godunov method introduced later on. The diaphragm represents the interface ...
00410233.pdf
... To ensure the same level of safeness then for today’s rolling stock, additional issues like Reynolds-Number and Mach-Number dependencies have to be explored. The influence of unsteady flow phenomena as well as the impact of the train’s induced flow field on humans and infrastructure has to be invest ...
... To ensure the same level of safeness then for today’s rolling stock, additional issues like Reynolds-Number and Mach-Number dependencies have to be explored. The influence of unsteady flow phenomena as well as the impact of the train’s induced flow field on humans and infrastructure has to be invest ...
GEF 2500 Problem set 3 U
... Couette flow implies that there is a moving plate at one boundary and a fixed plate at the other. It is a very common experimental configuration, and often used to determine fluid’s viscosity. Consider the flow of a viscous Newtonian fluid between two parallel plates located at and . The flow has cons ...
... Couette flow implies that there is a moving plate at one boundary and a fixed plate at the other. It is a very common experimental configuration, and often used to determine fluid’s viscosity. Consider the flow of a viscous Newtonian fluid between two parallel plates located at and . The flow has cons ...
CVE 304: Hydraulics II (2 Units)
... d) Rectangular, Triangular, Trapezoidal, Circular, Semi-Circular or irregular shape ...
... d) Rectangular, Triangular, Trapezoidal, Circular, Semi-Circular or irregular shape ...
Complex Geometries and Higher Reynolds Numbers
... x /(d Re) is dimensionless distance down the pipe. When this distance is infinite, Poiseuille flow is fully developed. If Re = 1, Poiseuille flow is well-developed in a short distance down the pipe: x/d = 1 → x = d = 2a (just 2 half-widths down the pipe). As the Reynolds number increases, this dista ...
... x /(d Re) is dimensionless distance down the pipe. When this distance is infinite, Poiseuille flow is fully developed. If Re = 1, Poiseuille flow is well-developed in a short distance down the pipe: x/d = 1 → x = d = 2a (just 2 half-widths down the pipe). As the Reynolds number increases, this dista ...
MA3842 - Fluid Dynamics. Question Sheet 6. Potential Flow. 1. (a
... the pressure is a minimum. Mark these points on a rough sketch of the flow. In which direction do you think the net force on the cylinder will act? 7. Fig. 1 shows a flow that is anti-parallel to the x axis at x → ∞, that encounters a wedge with an angle 2π/3. Use a suitable conformal mapping to rel ...
... the pressure is a minimum. Mark these points on a rough sketch of the flow. In which direction do you think the net force on the cylinder will act? 7. Fig. 1 shows a flow that is anti-parallel to the x axis at x → ∞, that encounters a wedge with an angle 2π/3. Use a suitable conformal mapping to rel ...
Magnetic Flow Meters Improve Recycling of Gas Well
... Magnetic Flow Meters Improve Recycling of Gas Well-produced Water Industry: Oil & Gas ...
... Magnetic Flow Meters Improve Recycling of Gas Well-produced Water Industry: Oil & Gas ...
Compressible flow

Compressible flow (gas dynamics) is the branch of fluid mechanics that deals with flows having significant changes in fluid density. Gases, but not liquids, display such behaviour. To distinguish between compressible and incompressible flow in air, the Mach number (the ratio of the speed of the flow to the speed of sound) must be greater than about 0.3 (since the density change is greater than 5% in that case) before significant compressibility occurs. The study of compressible flow is relevant to high-speed aircraft, jet engines, rocket motors, hyperloops, high-speed entry into a planetary atmosphere, gas pipelines, commercial applications such as abrasive blasting, and many other fields.