Quantum spin liquids as soft-
... Lattice translational symmetry is respected. The absence of long ranged magnetic order. ...
... Lattice translational symmetry is respected. The absence of long ranged magnetic order. ...
2.2 Schrödinger`s wave equation
... 2.2 Schrödinger’s wave equation Slides: Video 2.2.1 Schrödinger wave equation introduction Text reference: Quantum Mechanics for Scientists and Engineers Section Chapter 2 introduction ...
... 2.2 Schrödinger’s wave equation Slides: Video 2.2.1 Schrödinger wave equation introduction Text reference: Quantum Mechanics for Scientists and Engineers Section Chapter 2 introduction ...
Q 2
... (Frequently, physicists set c = 1 and quote mass and/or momentum in “GeV” units, as in the graph of the proton electric form factor, lecture 4. This is just a form of shorthand – they really mean GeV/c for momentum and GeV/c2 for mass.... numerically these have the same value because the value of c ...
... (Frequently, physicists set c = 1 and quote mass and/or momentum in “GeV” units, as in the graph of the proton electric form factor, lecture 4. This is just a form of shorthand – they really mean GeV/c for momentum and GeV/c2 for mass.... numerically these have the same value because the value of c ...
Memory-built-in quantum teleportation with photonic and atomic qubits
... fidelities for different initial states are all well beyond the classical limit of two-thirds, confirming the success of teleportation between photonic and atomic qubits. To show the ability to store the teleported state in our quantum memory, we further measure the fidelity of teleportation of righ ...
... fidelities for different initial states are all well beyond the classical limit of two-thirds, confirming the success of teleportation between photonic and atomic qubits. To show the ability to store the teleported state in our quantum memory, we further measure the fidelity of teleportation of righ ...
Radiative Transitions between Electronic States
... 4.4 Light as an Oscillating Electric Field Frequency () of oscillating field must “match” a possible electronic oscillation frequency (conservation of energy) There must be an interaction or coupling between the field (oscillating dipoles) and the electron Interaction strength depends on field ...
... 4.4 Light as an Oscillating Electric Field Frequency () of oscillating field must “match” a possible electronic oscillation frequency (conservation of energy) There must be an interaction or coupling between the field (oscillating dipoles) and the electron Interaction strength depends on field ...
PDF - at www.arxiv.org.
... The creation of a quantum computer is an outstanding fundamental and practical problem. The quantum computer could be used for the execution of very complicated tasks which are not solvable with the classical computers. The first prototype of a solid state quantum computer was created in 2009 with s ...
... The creation of a quantum computer is an outstanding fundamental and practical problem. The quantum computer could be used for the execution of very complicated tasks which are not solvable with the classical computers. The first prototype of a solid state quantum computer was created in 2009 with s ...
Comparison of Genetic Algorithm and Quantum Genetic Algorithm
... [7], a QGA was also used to solve the binary decision diagram ordering problem. More recently, QGA where used to evolve Cellular Automata rules (CA) [5, 6] to solve the density classification problem. In this work, we propose to make a comparison between GA and QGA to extract some computational abil ...
... [7], a QGA was also used to solve the binary decision diagram ordering problem. More recently, QGA where used to evolve Cellular Automata rules (CA) [5, 6] to solve the density classification problem. In this work, we propose to make a comparison between GA and QGA to extract some computational abil ...
Chapter 8 - Chemistry
... - a particular distribution of electrons among the available subshells - notation for configuration lists the subshell symbols, one after the other, with a subscript giving the number of electrons in that subshell eg. boron 1s2 2s2 2p1 orbital diagram - a diagram to show how the orbitals of a subshe ...
... - a particular distribution of electrons among the available subshells - notation for configuration lists the subshell symbols, one after the other, with a subscript giving the number of electrons in that subshell eg. boron 1s2 2s2 2p1 orbital diagram - a diagram to show how the orbitals of a subshe ...
Resonant Tunneling Between Quantum Hall Edge States
... [6] A. Furusaki and N. Nagaosa, Phys. Rev. B 47, 3827 (1993). [7] C. L. Kane and M. P. A. Fisher, Phys. Rev. B46, 7268 (1992); op. cit., 15233 (1992). [8] These tunneling paths (weak links) may be due to random impurity potentials or an intentionally created quantum dot. If the tunneling occurs thro ...
... [6] A. Furusaki and N. Nagaosa, Phys. Rev. B 47, 3827 (1993). [7] C. L. Kane and M. P. A. Fisher, Phys. Rev. B46, 7268 (1992); op. cit., 15233 (1992). [8] These tunneling paths (weak links) may be due to random impurity potentials or an intentionally created quantum dot. If the tunneling occurs thro ...
Quantum theory as a method: the epistemic
... ...nor is there “the” observable measured in a given setup,... • ...so there is no such thing as correctly assigning a quantum state. Problem: There is “correct” and “incorrect” in quantum state assignment in practice. Disanalogy between states and observables: States are updated after measurement, ...
... ...nor is there “the” observable measured in a given setup,... • ...so there is no such thing as correctly assigning a quantum state. Problem: There is “correct” and “incorrect” in quantum state assignment in practice. Disanalogy between states and observables: States are updated after measurement, ...
QIPC 2011
... 4. Universal Set of Quantum Gates • Quantum algorithms are specified as sequences of unitary transformations U1,U2, U3, each acting on a small number of qubits • Each U is generated by a time-dependent Hamiltonian: ...
... 4. Universal Set of Quantum Gates • Quantum algorithms are specified as sequences of unitary transformations U1,U2, U3, each acting on a small number of qubits • Each U is generated by a time-dependent Hamiltonian: ...
Quantum Statistics - Ole Witt
... 3. Canonical ensembles of quantum mechanical systems.......................................................... 5 4. An ideal gas consisting of non identical particles.................................................................. 8 5. The linear harmonic oscillator. Solid crystal materials....... ...
... 3. Canonical ensembles of quantum mechanical systems.......................................................... 5 4. An ideal gas consisting of non identical particles.................................................................. 8 5. The linear harmonic oscillator. Solid crystal materials....... ...
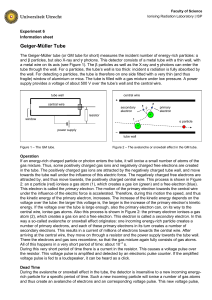
6 Geiger-Müller Tube - Ioniserende Stralen Practicum
... secondary electrons. This results in a current of millions of electrons towards the central wire. After arriving at the central wire, they move on through a resistor and the power supply towards the tube wall. There the electrons and gas ions recombine, so that the gas mixture again fully consists o ...
... secondary electrons. This results in a current of millions of electrons towards the central wire. After arriving at the central wire, they move on through a resistor and the power supply towards the tube wall. There the electrons and gas ions recombine, so that the gas mixture again fully consists o ...
Appendix E -‐ Elements of Quantum Mechanics
... Quantum mechanics provides a correct description of phenomena on the atomic or sub-‐atomic scale, where the ideas of classical mechanics are not generally applicable. As we describe nuclear phe ...
... Quantum mechanics provides a correct description of phenomena on the atomic or sub-‐atomic scale, where the ideas of classical mechanics are not generally applicable. As we describe nuclear phe ...
Quantum electrodynamics

In particle physics, quantum electrodynamics (QED) is the relativistic quantum field theory of electrodynamics. In essence, it describes how light and matter interact and is the first theory where full agreement between quantum mechanics and special relativity is achieved. QED mathematically describes all phenomena involving electrically charged particles interacting by means of exchange of photons and represents the quantum counterpart of classical electromagnetism giving a complete account of matter and light interaction.In technical terms, QED can be described as a perturbation theory of the electromagnetic quantum vacuum. Richard Feynman called it ""the jewel of physics"" for its extremely accurate predictions of quantities like the anomalous magnetic moment of the electron and the Lamb shift of the energy levels of hydrogen.