習題 - OoCities
... Suppose that we will randomly select a sample of n units from a population and that we will compute the sample proportion p of these units that fall into a category of interest. If we consider the sampling distribution of p: a. If the sample size n is large, the sampling distribution of p is approxi ...
... Suppose that we will randomly select a sample of n units from a population and that we will compute the sample proportion p of these units that fall into a category of interest. If we consider the sampling distribution of p: a. If the sample size n is large, the sampling distribution of p is approxi ...
40. INTRODUCTION TO t
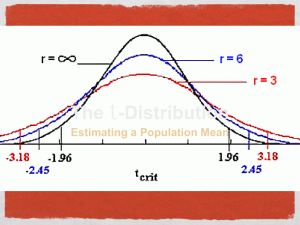
... t-Distribution When sample sizes are sometimes small, and often we do not know the standard deviation of the population, statisticians rely on the distribution of the t statistic (also known as the t score), whose values are given by: _ s X ± t* √n ...
... t-Distribution When sample sizes are sometimes small, and often we do not know the standard deviation of the population, statisticians rely on the distribution of the t statistic (also known as the t score), whose values are given by: _ s X ± t* √n ...
Statistics 101
... The mean income of the sample of households contacted by the Current Population Survey was $57,045. The number 57,045 is a statistic because it describes this one CPS sample. The population that the poll wants to draw conclusions about is all 106 million U.S. households. The parameter of interest is ...
... The mean income of the sample of households contacted by the Current Population Survey was $57,045. The number 57,045 is a statistic because it describes this one CPS sample. The population that the poll wants to draw conclusions about is all 106 million U.S. households. The parameter of interest is ...
Key Probability Distributions in Econometrics
... lower to the upper limit of the range. A couple of results to commit to memory are P (µ − 2σ < x < µ + 2σ ) ≈ 0.95 and P (µ − 3σ < x < µ + 3σ ) ≈ 0.997. A compact notation for saying that x is distributed normally with mean µ and variance σ 2 is x ∼ N(µ, σ 2 ). The χ 2 distribution represents the di ...
... lower to the upper limit of the range. A couple of results to commit to memory are P (µ − 2σ < x < µ + 2σ ) ≈ 0.95 and P (µ − 3σ < x < µ + 3σ ) ≈ 0.997. A compact notation for saying that x is distributed normally with mean µ and variance σ 2 is x ∼ N(µ, σ 2 ). The χ 2 distribution represents the di ...