SHM - Red Hook Central Schools
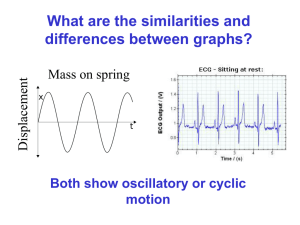
... EXAMPLE: A 4.0-kg mass is placed on a spring’s end and displaced 2.0 m to the right. The spring force F vs. its displacement x from equilibrium is shown in the graph. (b) Find the spring constant of the spring. SOLUTION: Use Hooke’s law: F = -kx. Pick any F and any x. Use k = -F / x. Thus k = -(-5 ...
... EXAMPLE: A 4.0-kg mass is placed on a spring’s end and displaced 2.0 m to the right. The spring force F vs. its displacement x from equilibrium is shown in the graph. (b) Find the spring constant of the spring. SOLUTION: Use Hooke’s law: F = -kx. Pick any F and any x. Use k = -F / x. Thus k = -(-5 ...
lectures 2014
... is the angular acceleration, θ . Can we find an equivalent to Newton’s second law for rotational mechanics, and if so, what is the equivalent of the mass, m ? ...
... is the angular acceleration, θ . Can we find an equivalent to Newton’s second law for rotational mechanics, and if so, what is the equivalent of the mass, m ? ...
Systems of particles
... So far, we have discussed only the application of Newton’s laws to particles, or to bodies in situations where they can be treated as particles — planets in orbit round the Sun, for example. In this chapter, we apply Newton’s laws to systems of interacting particles, which could be as simple as two ...
... So far, we have discussed only the application of Newton’s laws to particles, or to bodies in situations where they can be treated as particles — planets in orbit round the Sun, for example. In this chapter, we apply Newton’s laws to systems of interacting particles, which could be as simple as two ...
Workdone, Energy and Power
... (a) a body of mass 5kg moving with speed 4 ms−1 (b) a body of mass 2kg moving with speed 3 ms−1 (c) a car of mass 800kg moving with speed 10 ms−1 (d) a bullet of mass 10g moving with speed 400 ms−1 2. Find the potential energy gained by: (a) a body of mass 5kg raised through a vertical distance of 1 ...
... (a) a body of mass 5kg moving with speed 4 ms−1 (b) a body of mass 2kg moving with speed 3 ms−1 (c) a car of mass 800kg moving with speed 10 ms−1 (d) a bullet of mass 10g moving with speed 400 ms−1 2. Find the potential energy gained by: (a) a body of mass 5kg raised through a vertical distance of 1 ...
File
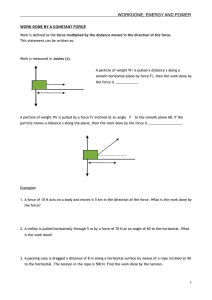
... • The amount of work done, force and distance are related by the equation: work done = force applied × distance moved in direction of force • Work done against frictional forces is mainly transformed into heat. • Elastic potential is the energy stored in an object when work is done on the object to ...
... • The amount of work done, force and distance are related by the equation: work done = force applied × distance moved in direction of force • Work done against frictional forces is mainly transformed into heat. • Elastic potential is the energy stored in an object when work is done on the object to ...
Monday, April 7, 2008 - UTA HEP WWW Home Page
... The principle of energy conservation can be used to solve problems that are harder to solve just using Newton’s laws. It is used to describe motion of an object or a system of objects. A new concept of linear momentum can also be used to solve physical problems, especially the problems involving col ...
... The principle of energy conservation can be used to solve problems that are harder to solve just using Newton’s laws. It is used to describe motion of an object or a system of objects. A new concept of linear momentum can also be used to solve physical problems, especially the problems involving col ...