Chapter 6 Momentum and Impulse
... equal in magnitude and opposite in direction, and the time of contact is the same for each of the bodies, the impulse of FABis equal in magnitude and opposite in direction to the impulse of FBA. If the force is constant, the area under the curve is given by the product of the magnitude of the force ...
... equal in magnitude and opposite in direction, and the time of contact is the same for each of the bodies, the impulse of FABis equal in magnitude and opposite in direction to the impulse of FBA. If the force is constant, the area under the curve is given by the product of the magnitude of the force ...
A 0.300 kg ball is thrown at a frictionless wall, at a 30o angle with
... separate inner tubes, tied together by a 10 m rope. Arnold was 2 times heavier and about 4 times stronger. A floating cooler had drifted to halfway between them, and they start a playful tug of war to get to the cooler. Who gets to the cooler first? ...
... separate inner tubes, tied together by a 10 m rope. Arnold was 2 times heavier and about 4 times stronger. A floating cooler had drifted to halfway between them, and they start a playful tug of war to get to the cooler. Who gets to the cooler first? ...
PSI AP Physics I
... 1. Which variable has more impact on an object’s motion? Its mass or its velocity? 2. Is momentum a vector or a scalar? Explain. 3. Why does changing the duration of an impulse on an object change the force exerted on the object so radically? 4. What is the value of air bags in cars and trucks? 5. W ...
... 1. Which variable has more impact on an object’s motion? Its mass or its velocity? 2. Is momentum a vector or a scalar? Explain. 3. Why does changing the duration of an impulse on an object change the force exerted on the object so radically? 4. What is the value of air bags in cars and trucks? 5. W ...
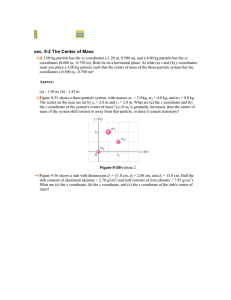
Center of Mass and Linear Momentum
... Answer: The system consists of Fred, Ethel and the pole. All forces are internal. Therefore the com will remain in the same place. Since the origin is the com, they will meet at the origin in all three cases! (Of course the origin where the com is located is closer to Fred than to ...
... Answer: The system consists of Fred, Ethel and the pole. All forces are internal. Therefore the com will remain in the same place. Since the origin is the com, they will meet at the origin in all three cases! (Of course the origin where the com is located is closer to Fred than to ...
Ch# 9 - KFUPM Faculty List
... Q9: A 1.0 kg ball strikes a vertical wall at an angle of 30 degrees with a speed of 3.0 m/s and bounces off at the same angle with the same speed, as shown in Fig 4. The change in momentum of the ball is : (Ans 3 kg*m/s to the left) Q10: A 6.0 kg body moving with velocity v breaks up (explodes) into ...
... Q9: A 1.0 kg ball strikes a vertical wall at an angle of 30 degrees with a speed of 3.0 m/s and bounces off at the same angle with the same speed, as shown in Fig 4. The change in momentum of the ball is : (Ans 3 kg*m/s to the left) Q10: A 6.0 kg body moving with velocity v breaks up (explodes) into ...
IGCSE-14-Momentum
... velocity to fall to zero. The time taken for their passenger’s ________ momentum to fall to ______zero is also increased. Therefore the _______ exertedforce on the driver or passenger is __________ decreased injury and so is the potential ________ caused. WORD SELECTION: time velocity zero momentum ...
... velocity to fall to zero. The time taken for their passenger’s ________ momentum to fall to ______zero is also increased. Therefore the _______ exertedforce on the driver or passenger is __________ decreased injury and so is the potential ________ caused. WORD SELECTION: time velocity zero momentum ...
Elastic Collision
... define momentum as a vector quantity equal to the product of the mass and the velocity of an object explain, quantitatively, the concepts of impulse and change in momentum, using Newton’s laws of motion explain, qualitatively, that momentum is conserved in an isolated system explain, quantit ...
... define momentum as a vector quantity equal to the product of the mass and the velocity of an object explain, quantitatively, the concepts of impulse and change in momentum, using Newton’s laws of motion explain, qualitatively, that momentum is conserved in an isolated system explain, quantit ...