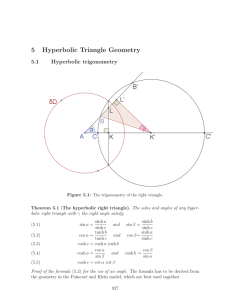
- Miskolc Mathematical Notes
... we shortly discuss how the ideas from the previous subsection can be used to make the nonobtuse triangulation from the coarse triangulation, with obtuse triangles in it, built by the grid generator. So far, various refinement techniques proposed – red, yellow, and yellow-red – are only applied to th ...
... we shortly discuss how the ideas from the previous subsection can be used to make the nonobtuse triangulation from the coarse triangulation, with obtuse triangles in it, built by the grid generator. So far, various refinement techniques proposed – red, yellow, and yellow-red – are only applied to th ...
triangles in neutral geometry three theorems of measurement lesson
... 3. given a triangle ABC, consider the interior and exterior angles at a vertex, say vertex A. Prove that the bisectors of those two angles are perpendicular. 4. Prove that for any point P and line , there are points on which are arbitrarily far away from . 5. Prove that equilateral triangles ex ...
... 3. given a triangle ABC, consider the interior and exterior angles at a vertex, say vertex A. Prove that the bisectors of those two angles are perpendicular. 4. Prove that for any point P and line , there are points on which are arbitrarily far away from . 5. Prove that equilateral triangles ex ...
Chapter 4 Notes
... Given : DUK is an isosceles triangle with DU and DK as legs. 1 and 2 are right angles. Pr ove : U K ...
... Given : DUK is an isosceles triangle with DU and DK as legs. 1 and 2 are right angles. Pr ove : U K ...
Triangles - Study Point
... The triangle may be acute, obtuse, or right, the angle bisectors of a triangle must meet at a point lying inside the triangle. (iii) The incentre of a triangle lies in the interior of the triangle. (iv) The bisectors of the angles of a triangle are concurrent. (v) From the incentre we can draw a o ...
... The triangle may be acute, obtuse, or right, the angle bisectors of a triangle must meet at a point lying inside the triangle. (iii) The incentre of a triangle lies in the interior of the triangle. (iv) The bisectors of the angles of a triangle are concurrent. (v) From the incentre we can draw a o ...
Chapter 13 Geometry
... obtain x via an application of the Pythagorean theorem. The arc length of the shorter walk around the circle can be obtained from angle a of this triangle. The arc we are interested in is defined by the angle 2a (in radians), and so is (2a)/(2π) times the total circumference of the circle, which is ...
... obtain x via an application of the Pythagorean theorem. The arc length of the shorter walk around the circle can be obtained from angle a of this triangle. The arc we are interested in is defined by the angle 2a (in radians), and so is (2a)/(2π) times the total circumference of the circle, which is ...
Angles in Polygons
... lesson, students will find that the length of two sides and the measure of the angle between the two sides describes a unique triangle. Also, knowing the three sides of a triangle will result in a unique triangle, as long as the three sides connect to make a triangle. Students will find that there a ...
... lesson, students will find that the length of two sides and the measure of the angle between the two sides describes a unique triangle. Also, knowing the three sides of a triangle will result in a unique triangle, as long as the three sides connect to make a triangle. Students will find that there a ...
Angles and Triangles
... Another relationship exists between the angles and the sides of a triangle. In a triangle, the side opposite the angle with the greatest measure is the longest side. 9. Compare the angle measure to the side opposite the angle in a scalene triangle. What is true about the side opposite the angle w ...
... Another relationship exists between the angles and the sides of a triangle. In a triangle, the side opposite the angle with the greatest measure is the longest side. 9. Compare the angle measure to the side opposite the angle in a scalene triangle. What is true about the side opposite the angle w ...
Incircle and excircles of a triangle
Incircle redirects here. For incircles of non-triangle polygons, see Tangential quadrilateral or Tangential polygon.In geometry, the incircle or inscribed circle of a triangle is the largest circle contained in the triangle; it touches (is tangent to) the three sides. The center of the incircle is called the triangle's incenter.An excircle or escribed circle of the triangle is a circle lying outside the triangle, tangent to one of its sides and tangent to the extensions of the other two. Every triangle has three distinct excircles, each tangent to one of the triangle's sides.The center of the incircle, called the incenter, can be found as the intersection of the three internal angle bisectors. The center of an excircle is the intersection of the internal bisector of one angle (at vertex A, for example) and the external bisectors of the other two. The center of this excircle is called the excenter relative to the vertex A, or the excenter of A. Because the internal bisector of an angle is perpendicular to its external bisector, it follows that the center of the incircle together with the three excircle centers form an orthocentric system.Polygons with more than three sides do not all have an incircle tangent to all sides; those that do are called tangential polygons. See also Tangent lines to circles.