On existence of a triangle with prescribed bisector lengths
... triangles with prescribed its three elements. In particular, a triangle with given lengths of its sides can be constructed if the ‘triangle inequalities’ are fulfilled and then the triangle is unique up to an isometry. In a similar way, the problems of constructing a triangle with given lengths of i ...
... triangles with prescribed its three elements. In particular, a triangle with given lengths of its sides can be constructed if the ‘triangle inequalities’ are fulfilled and then the triangle is unique up to an isometry. In a similar way, the problems of constructing a triangle with given lengths of i ...
Packet 1 for Unit 6 M2G
... ASSIGNMENT SHEET FOR PACKET 1 OF UNIT 6 This packet includes sections 5-1, 5-2, and 5-3 from our textbook and the review for those ...
... ASSIGNMENT SHEET FOR PACKET 1 OF UNIT 6 This packet includes sections 5-1, 5-2, and 5-3 from our textbook and the review for those ...
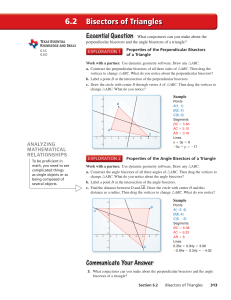
Bisectors of Triangles 6.2
... official hockey rink used by the National Hockey League. Create a triangle using hockey players as vertices in which the center circle is inscribed in the triangle. The center dot should be the incenter of your triangle. Sketch a drawing of the locations of your hockey players. Then label the actual ...
... official hockey rink used by the National Hockey League. Create a triangle using hockey players as vertices in which the center circle is inscribed in the triangle. The center dot should be the incenter of your triangle. Sketch a drawing of the locations of your hockey players. Then label the actual ...
1 - Angelfire
... side. The perimeter of the entrance is 14 feet. Find each side length. of a frame is 6 _1_ inches long. How many ...
... side. The perimeter of the entrance is 14 feet. Find each side length. of a frame is 6 _1_ inches long. How many ...
Dependent - Gerry Stahl`s Home Page
... (points, lines and circles). It is becoming visually confusing. That is why it is often useful to package all of this in a special tool, which hides the underlying ...
... (points, lines and circles). It is becoming visually confusing. That is why it is often useful to package all of this in a special tool, which hides the underlying ...
Classifying Polygons
... Know What? Revisited The pentagon is divided up into 10 sections, all quadrilaterals. More specifically, there are 5 rectangles and 5 kites. None of these dividing lines are diagonals because they are not drawn from vertices. ...
... Know What? Revisited The pentagon is divided up into 10 sections, all quadrilaterals. More specifically, there are 5 rectangles and 5 kites. None of these dividing lines are diagonals because they are not drawn from vertices. ...
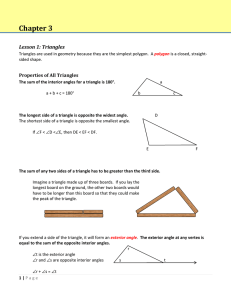
155 6–2 Triangles Interior Angles of a Polygon
... 7. Two streets, one 16.2 m and the other 31.5 m wide, cross at right angles. What is the diagonal distance between the opposite corners? ...
... 7. Two streets, one 16.2 m and the other 31.5 m wide, cross at right angles. What is the diagonal distance between the opposite corners? ...
Print › Geometry Ch 4 Fitch FMS | Quizlet | Quizlet
... Angle-Angle-Side (AAS) Congruence Postulate: If 2 angles and a non-included side of one triangle are congruent to 2 angles and the corresponding non-included side of another, then the 2 triangles are congruent ...
... Angle-Angle-Side (AAS) Congruence Postulate: If 2 angles and a non-included side of one triangle are congruent to 2 angles and the corresponding non-included side of another, then the 2 triangles are congruent ...
Student Name
... D. Triangle PQS is a reflection of triangle RQT, so the triangles are congruent by AAA. 12. Which sequence of transformations will result in an image that is NOT congruent to graphed on the coordinate grid below? ...
... D. Triangle PQS is a reflection of triangle RQT, so the triangles are congruent by AAA. 12. Which sequence of transformations will result in an image that is NOT congruent to graphed on the coordinate grid below? ...
State whether each sentence is true or false . If false
... 1. The centroid is the point at which the altitudes of a triangle intersect. SOLUTION: The centroid is the the point where the medians intersect. The orthocenter is the point where the altitudes intersect. false; orthocenter 2. The point of concurrency of the medians of a triangle is called the in ...
... 1. The centroid is the point at which the altitudes of a triangle intersect. SOLUTION: The centroid is the the point where the medians intersect. The orthocenter is the point where the altitudes intersect. false; orthocenter 2. The point of concurrency of the medians of a triangle is called the in ...
Incircle and excircles of a triangle
Incircle redirects here. For incircles of non-triangle polygons, see Tangential quadrilateral or Tangential polygon.In geometry, the incircle or inscribed circle of a triangle is the largest circle contained in the triangle; it touches (is tangent to) the three sides. The center of the incircle is called the triangle's incenter.An excircle or escribed circle of the triangle is a circle lying outside the triangle, tangent to one of its sides and tangent to the extensions of the other two. Every triangle has three distinct excircles, each tangent to one of the triangle's sides.The center of the incircle, called the incenter, can be found as the intersection of the three internal angle bisectors. The center of an excircle is the intersection of the internal bisector of one angle (at vertex A, for example) and the external bisectors of the other two. The center of this excircle is called the excenter relative to the vertex A, or the excenter of A. Because the internal bisector of an angle is perpendicular to its external bisector, it follows that the center of the incircle together with the three excircle centers form an orthocentric system.Polygons with more than three sides do not all have an incircle tangent to all sides; those that do are called tangential polygons. See also Tangent lines to circles.