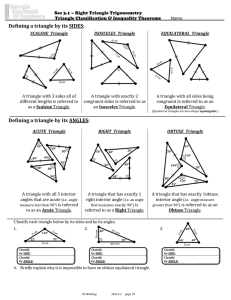
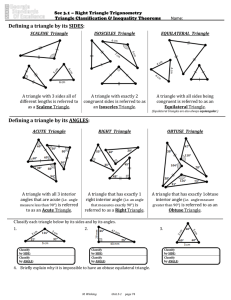
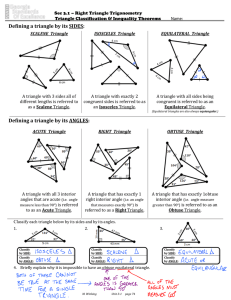
Defining a triangle by its ANGLES
... Sec 3.1 – Right Triangle Trigonometry Triangle Classification & Inequality Theorems ...
... Sec 3.1 – Right Triangle Trigonometry Triangle Classification & Inequality Theorems ...
Unit 5 Packet
... Using the points given, draw each midsegment. Then show that the midsegments are parallel and ½ the length of the sides. 9. A(1, 3) B(3, -1) C(5, 3) 10. D(-2, 3) E(4, 5) F(0, -3) ...
... Using the points given, draw each midsegment. Then show that the midsegments are parallel and ½ the length of the sides. 9. A(1, 3) B(3, -1) C(5, 3) 10. D(-2, 3) E(4, 5) F(0, -3) ...
Target 5a (Day 1)
... equidistant from the ______________ of the segment. Theorem 5.2 – Any point _________________ from the endpoints of a segment _______ on the perpendicular bisector of the segment. Concurrent lines – When ___ or more lines intersect at a common point. Point of Concurrency – The ________________ point ...
... equidistant from the ______________ of the segment. Theorem 5.2 – Any point _________________ from the endpoints of a segment _______ on the perpendicular bisector of the segment. Concurrent lines – When ___ or more lines intersect at a common point. Point of Concurrency – The ________________ point ...
Geometry Playground Activity Comparing Constructions in Spherical
... Begin Geometry Playground and select the Spherical tab to start a new session in spherical geometry. Construct three points using the Construct → Points tool, and then connect them to form a triangle using the Construct → Lines tool. 1. What do you notice about the appearance of the lines in your tr ...
... Begin Geometry Playground and select the Spherical tab to start a new session in spherical geometry. Construct three points using the Construct → Points tool, and then connect them to form a triangle using the Construct → Lines tool. 1. What do you notice about the appearance of the lines in your tr ...
Incircle and excircles of a triangle
Incircle redirects here. For incircles of non-triangle polygons, see Tangential quadrilateral or Tangential polygon.In geometry, the incircle or inscribed circle of a triangle is the largest circle contained in the triangle; it touches (is tangent to) the three sides. The center of the incircle is called the triangle's incenter.An excircle or escribed circle of the triangle is a circle lying outside the triangle, tangent to one of its sides and tangent to the extensions of the other two. Every triangle has three distinct excircles, each tangent to one of the triangle's sides.The center of the incircle, called the incenter, can be found as the intersection of the three internal angle bisectors. The center of an excircle is the intersection of the internal bisector of one angle (at vertex A, for example) and the external bisectors of the other two. The center of this excircle is called the excenter relative to the vertex A, or the excenter of A. Because the internal bisector of an angle is perpendicular to its external bisector, it follows that the center of the incircle together with the three excircle centers form an orthocentric system.Polygons with more than three sides do not all have an incircle tangent to all sides; those that do are called tangential polygons. See also Tangent lines to circles.