Chapter 4 Notes
... Postulate - ASA – If two angles and the included side of one triangle are congruent to the corresponding two angles and the included side of another triangle, then the two triangles are congruent. Theorem - AAS – If two angles and a nonincluded side of one triangle are congruent to the corresponding ...
... Postulate - ASA – If two angles and the included side of one triangle are congruent to the corresponding two angles and the included side of another triangle, then the two triangles are congruent. Theorem - AAS – If two angles and a nonincluded side of one triangle are congruent to the corresponding ...
Advanced Trigonometry (1) Right Triangles of Equal Perimeter (2
... (26) BONUS Problem: Cut of Minimal Length That Splits Triangle into 2 Equal Pieces ...
... (26) BONUS Problem: Cut of Minimal Length That Splits Triangle into 2 Equal Pieces ...
6_Perpendicular_bisector
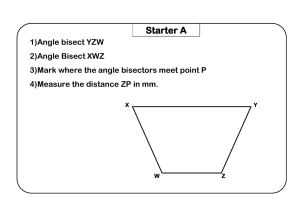
... 2)Angle Bisect XWZ 3)Mark where the angle bisectors meet point P 4)Measure the distance ZP in mm. X ...
... 2)Angle Bisect XWZ 3)Mark where the angle bisectors meet point P 4)Measure the distance ZP in mm. X ...
Geometer`s Sketchpad: Defining Triangles
... Q1: Which of the triangles seem the most flexible? Explain (Meaning: which triangle can you change all the angles?) Q2: Which of the triangles seems the least flexible? Explain. 6) Measure the angles in Triangle ABC. a. To measure an angle, select three points while holding the shift key, with the v ...
... Q1: Which of the triangles seem the most flexible? Explain (Meaning: which triangle can you change all the angles?) Q2: Which of the triangles seems the least flexible? Explain. 6) Measure the angles in Triangle ABC. a. To measure an angle, select three points while holding the shift key, with the v ...
Incircle and excircles of a triangle
Incircle redirects here. For incircles of non-triangle polygons, see Tangential quadrilateral or Tangential polygon.In geometry, the incircle or inscribed circle of a triangle is the largest circle contained in the triangle; it touches (is tangent to) the three sides. The center of the incircle is called the triangle's incenter.An excircle or escribed circle of the triangle is a circle lying outside the triangle, tangent to one of its sides and tangent to the extensions of the other two. Every triangle has three distinct excircles, each tangent to one of the triangle's sides.The center of the incircle, called the incenter, can be found as the intersection of the three internal angle bisectors. The center of an excircle is the intersection of the internal bisector of one angle (at vertex A, for example) and the external bisectors of the other two. The center of this excircle is called the excenter relative to the vertex A, or the excenter of A. Because the internal bisector of an angle is perpendicular to its external bisector, it follows that the center of the incircle together with the three excircle centers form an orthocentric system.Polygons with more than three sides do not all have an incircle tangent to all sides; those that do are called tangential polygons. See also Tangent lines to circles.