Full text
... In order to compute the delay through this circuit, it is necessary to compute the. resistance and capacitance between ground and the output. This note concentrates on the resistance. The approximation made in computing resistance in this paper is that each transistor with a high input is in the con ...
... In order to compute the delay through this circuit, it is necessary to compute the. resistance and capacitance between ground and the output. This note concentrates on the resistance. The approximation made in computing resistance in this paper is that each transistor with a high input is in the con ...
Example
... • Computers do not use the decimal system in computations and memory but use the binary system • It caused by computer memory consists of a huge number of electronic and magnetic recording devices, of which each element has only “on” and “off” statuses ...
... • Computers do not use the decimal system in computations and memory but use the binary system • It caused by computer memory consists of a huge number of electronic and magnetic recording devices, of which each element has only “on” and “off” statuses ...
ppt
... • Convert column-to-row and back with transpose (’) • Can access the same way as row vectors ...
... • Convert column-to-row and back with transpose (’) • Can access the same way as row vectors ...
COP 3223 Section 1 Spring 2017 Exam 2 Review
... Full Disclosure: I am not the professor, and I am not making your real exam. This test is strictly for practice. This test may cover more, or even less than what is on the actual test. This test is my best guess of what would be important to study. A student with questions about the content of the a ...
... Full Disclosure: I am not the professor, and I am not making your real exam. This test is strictly for practice. This test may cover more, or even less than what is on the actual test. This test is my best guess of what would be important to study. A student with questions about the content of the a ...
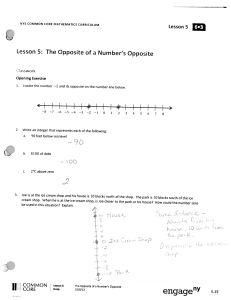
Probability 1 1. What is the probability that a randomly drawn
... 10. A point P is randomly selected from the rectangular region with vertices (0, 0), (2, 0), (2, 1), (0, 1). What is the probability that P is closer to the origin than it is to the point (3, 1)? (A) ...
... 10. A point P is randomly selected from the rectangular region with vertices (0, 0), (2, 0), (2, 1), (0, 1). What is the probability that P is closer to the origin than it is to the point (3, 1)? (A) ...
lesson-4modular-arithmetric1
... Definition 6a: Additive Identity Element and Additive Inverse In the table above for +5, we see that any element in 5 , say a, a +5 0 = a and 0 +5 a = a. We say that 0 is the additive identity element in 5. We also notice that 1 +5 4 = 0 , 4 +5 1 = 0, 2 +5 3 = 0 and 3 +5 2 = 0. We say that 1 is th ...
... Definition 6a: Additive Identity Element and Additive Inverse In the table above for +5, we see that any element in 5 , say a, a +5 0 = a and 0 +5 a = a. We say that 0 is the additive identity element in 5. We also notice that 1 +5 4 = 0 , 4 +5 1 = 0, 2 +5 3 = 0 and 3 +5 2 = 0. We say that 1 is th ...
MM2009 Maths Methods 2
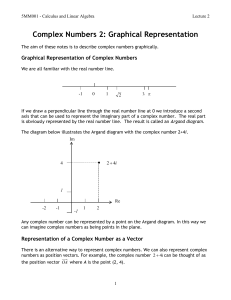
... We can also represent complex numbers as free vectors. The advantage of vector representation means that addition of complex numbers is then equivalent to the addition of the corresponding vectors. If z1 x1 y1i and z 2 x2 y2i then z1 z 2 x1 x2 y1 y2 i and z1 z 2 will form ...
... We can also represent complex numbers as free vectors. The advantage of vector representation means that addition of complex numbers is then equivalent to the addition of the corresponding vectors. If z1 x1 y1i and z 2 x2 y2i then z1 z 2 x1 x2 y1 y2 i and z1 z 2 will form ...
Addition
Addition (often signified by the plus symbol ""+"") is one of the four elementary, mathematical operations of arithmetic, with the others being subtraction, multiplication and division.The addition of two whole numbers is the total amount of those quantities combined. For example, in the picture on the right, there is a combination of three apples and two apples together; making a total of 5 apples. This observation is equivalent to the mathematical expression ""3 + 2 = 5"" i.e., ""3 add 2 is equal to 5"".Besides counting fruits, addition can also represent combining other physical objects. Using systematic generalizations, addition can also be defined on more abstract quantities, such as integers, rational numbers, real numbers and complex numbers and other abstract objects such as vectors and matrices.In arithmetic, rules for addition involving fractions and negative numbers have been devised amongst others. In algebra, addition is studied more abstractly.Addition has several important properties. It is commutative, meaning that order does not matter, and it is associative, meaning that when one adds more than two numbers, the order in which addition is performed does not matter (see Summation). Repeated addition of 1 is the same as counting; addition of 0 does not change a number. Addition also obeys predictable rules concerning related operations such as subtraction and multiplication.Performing addition is one of the simplest numerical tasks. Addition of very small numbers is accessible to toddlers; the most basic task, 1 + 1, can be performed by infants as young as five months and even some non-human animals. In primary education, students are taught to add numbers in the decimal system, starting with single digits and progressively tackling more difficult problems. Mechanical aids range from the ancient abacus to the modern computer, where research on the most efficient implementations of addition continues to this day.