ppt
... another common use of hex numbers are to represent colours recall our discussion about colour models, in particular, the RGB (Red-Green-Blue) model a copy of the relevant slide from the Terminology III slides has been included here, for convenience ...
... another common use of hex numbers are to represent colours recall our discussion about colour models, in particular, the RGB (Red-Green-Blue) model a copy of the relevant slide from the Terminology III slides has been included here, for convenience ...
ppt
... sign extension restores some of them –16-bit -4ten to 32-bit: 1111 1111 1111 1100two 1111 1111 1111 1111 1111 1111 1111 1100two cs61c-f00 L3 9/6 ...
... sign extension restores some of them –16-bit -4ten to 32-bit: 1111 1111 1111 1100two 1111 1111 1111 1111 1111 1111 1111 1100two cs61c-f00 L3 9/6 ...
Booklet 5 - Suffolk Maths
... Ian was entering a Math contest for Grade 9. He was working on this particular problem. He was having difficulty with the answer. This was the problem: The integers greater than 1 are arranged, four in each row, in 5 columns, as follows: a ...
... Ian was entering a Math contest for Grade 9. He was working on this particular problem. He was having difficulty with the answer. This was the problem: The integers greater than 1 are arranged, four in each row, in 5 columns, as follows: a ...
Slide 1
... • How to compute A – B ? – Compute the 1’s complement of B (say, B1). – Compute R = A + B1 – If the carry obtained after addition is ‘1’ • Add the carry back to R (called end-around carry). • That is, R = R + 1. • The result is a positive number. ...
... • How to compute A – B ? – Compute the 1’s complement of B (say, B1). – Compute R = A + B1 – If the carry obtained after addition is ‘1’ • Add the carry back to R (called end-around carry). • That is, R = R + 1. • The result is a positive number. ...
mc_fp2-ch - WordPress.com
... Know that every non-zero complex number has n nth roots, and that in the Argand diagram these are the vertices of a regular n-gon. ...
... Know that every non-zero complex number has n nth roots, and that in the Argand diagram these are the vertices of a regular n-gon. ...
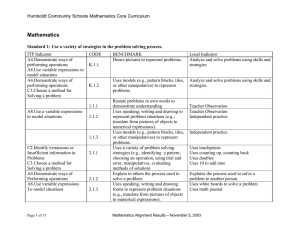
Math - Humboldt Community School District
... decimals and vice versa Decides appropriate units of measure to measure a variety of real world objects and situations Understand the basic laws of exponents Writes and evaluates expressions with ...
... decimals and vice versa Decides appropriate units of measure to measure a variety of real world objects and situations Understand the basic laws of exponents Writes and evaluates expressions with ...
Guidelines for Standards-Based Instruction
... sampling) and which method makes a sample more representative for a Population. 6 SDAP 2.3 Analyze data displays and explain why the way in which the question was asked might have influenced the results obtained and why the way in which the results were displayed might have influenced the conclusion ...
... sampling) and which method makes a sample more representative for a Population. 6 SDAP 2.3 Analyze data displays and explain why the way in which the question was asked might have influenced the results obtained and why the way in which the results were displayed might have influenced the conclusion ...
Addition
Addition (often signified by the plus symbol ""+"") is one of the four elementary, mathematical operations of arithmetic, with the others being subtraction, multiplication and division.The addition of two whole numbers is the total amount of those quantities combined. For example, in the picture on the right, there is a combination of three apples and two apples together; making a total of 5 apples. This observation is equivalent to the mathematical expression ""3 + 2 = 5"" i.e., ""3 add 2 is equal to 5"".Besides counting fruits, addition can also represent combining other physical objects. Using systematic generalizations, addition can also be defined on more abstract quantities, such as integers, rational numbers, real numbers and complex numbers and other abstract objects such as vectors and matrices.In arithmetic, rules for addition involving fractions and negative numbers have been devised amongst others. In algebra, addition is studied more abstractly.Addition has several important properties. It is commutative, meaning that order does not matter, and it is associative, meaning that when one adds more than two numbers, the order in which addition is performed does not matter (see Summation). Repeated addition of 1 is the same as counting; addition of 0 does not change a number. Addition also obeys predictable rules concerning related operations such as subtraction and multiplication.Performing addition is one of the simplest numerical tasks. Addition of very small numbers is accessible to toddlers; the most basic task, 1 + 1, can be performed by infants as young as five months and even some non-human animals. In primary education, students are taught to add numbers in the decimal system, starting with single digits and progressively tackling more difficult problems. Mechanical aids range from the ancient abacus to the modern computer, where research on the most efficient implementations of addition continues to this day.