§5.1 Exponents and Scientific Notation Definition of an exponent ar
... Now, for the next step with scientific notation – it can used to multiply and divide large/small numbers. This is really quite easy. Here is some explanation and how we can do it! What happens if we wish to do the following problem, 7 x 102 x 103 = (7 x 102)(1 x 103) We can think of 102 and 103 as " ...
... Now, for the next step with scientific notation – it can used to multiply and divide large/small numbers. This is really quite easy. Here is some explanation and how we can do it! What happens if we wish to do the following problem, 7 x 102 x 103 = (7 x 102)(1 x 103) We can think of 102 and 103 as " ...
The Complex Roots of a Quadratic Equation: A Visualization
... The graph of the modulus of p(z) is admirably suited to depicting its zeros whether they are real or complex; moreover, this graph is reasonably easy to draw with the right technological tools. Since the modulus of p(z), u = |p(z)|, is a real number, its graph is just a surface in space called the m ...
... The graph of the modulus of p(z) is admirably suited to depicting its zeros whether they are real or complex; moreover, this graph is reasonably easy to draw with the right technological tools. Since the modulus of p(z), u = |p(z)|, is a real number, its graph is just a surface in space called the m ...
Secrets of Fusion. where the two rivers meet
... Life Cycle { 9 Months, 90 Months Childhood, 900 Months Adult = ...
... Life Cycle { 9 Months, 90 Months Childhood, 900 Months Adult = ...
document
... Find the upper and lower bounds of simple calculations involving quantities given to a particular degree of accuracy Find the upper and lower bounds of more difficult calculations with quantities given to a various degrees of accuracy ...
... Find the upper and lower bounds of simple calculations involving quantities given to a particular degree of accuracy Find the upper and lower bounds of more difficult calculations with quantities given to a various degrees of accuracy ...
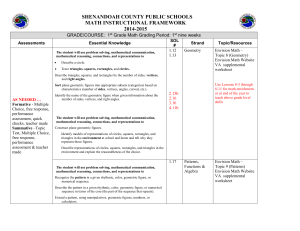
Assessments - Shenandoah County Public Schools
... Skip count orally by twos, fives and tens to 100 starting at various multiples of 2, 5, or 10. Count backward by ones from 30. The student will use problem solving, mathematical communication, mathematical reasoning, connections, and representations to Recognize the pattern in a given rhythmic, ...
... Skip count orally by twos, fives and tens to 100 starting at various multiples of 2, 5, or 10. Count backward by ones from 30. The student will use problem solving, mathematical communication, mathematical reasoning, connections, and representations to Recognize the pattern in a given rhythmic, ...
Basic Concepts of Discrete Probability
... Coding and Encryption: Mathematical Background • The most popular techniques of errorcorrecting coding and encryption are based on the specific operations defined on the set of integer numbers and on some specific properties of integer numbers, which are studied in detail in the Number Theory. • He ...
... Coding and Encryption: Mathematical Background • The most popular techniques of errorcorrecting coding and encryption are based on the specific operations defined on the set of integer numbers and on some specific properties of integer numbers, which are studied in detail in the Number Theory. • He ...
ppt
... another common use of hex numbers are to represent colours recall our discussion about colour models, in particular, the RGB (Red-Green-Blue) model a copy of the relevant slide from the Terminology III slides has been included here, for convenience ...
... another common use of hex numbers are to represent colours recall our discussion about colour models, in particular, the RGB (Red-Green-Blue) model a copy of the relevant slide from the Terminology III slides has been included here, for convenience ...
Addition
Addition (often signified by the plus symbol ""+"") is one of the four elementary, mathematical operations of arithmetic, with the others being subtraction, multiplication and division.The addition of two whole numbers is the total amount of those quantities combined. For example, in the picture on the right, there is a combination of three apples and two apples together; making a total of 5 apples. This observation is equivalent to the mathematical expression ""3 + 2 = 5"" i.e., ""3 add 2 is equal to 5"".Besides counting fruits, addition can also represent combining other physical objects. Using systematic generalizations, addition can also be defined on more abstract quantities, such as integers, rational numbers, real numbers and complex numbers and other abstract objects such as vectors and matrices.In arithmetic, rules for addition involving fractions and negative numbers have been devised amongst others. In algebra, addition is studied more abstractly.Addition has several important properties. It is commutative, meaning that order does not matter, and it is associative, meaning that when one adds more than two numbers, the order in which addition is performed does not matter (see Summation). Repeated addition of 1 is the same as counting; addition of 0 does not change a number. Addition also obeys predictable rules concerning related operations such as subtraction and multiplication.Performing addition is one of the simplest numerical tasks. Addition of very small numbers is accessible to toddlers; the most basic task, 1 + 1, can be performed by infants as young as five months and even some non-human animals. In primary education, students are taught to add numbers in the decimal system, starting with single digits and progressively tackling more difficult problems. Mechanical aids range from the ancient abacus to the modern computer, where research on the most efficient implementations of addition continues to this day.