Probability Theory
... He bet on a roll of a die that at least one 6 would appear during a total of four rolls. From past experience, he knew that he was more successful than not with this game of chance. Tired of his approach, he decided to change the game. He bet that he would get a total of 12, or a double 6, on twenty ...
... He bet on a roll of a die that at least one 6 would appear during a total of four rolls. From past experience, he knew that he was more successful than not with this game of chance. Tired of his approach, he decided to change the game. He bet that he would get a total of 12, or a double 6, on twenty ...
Welcome to our seventh seminar!
... The probability that there will be at least on successful outcome is the sum probability of the first event and second event occurring minus the probablity that both will occur P(A and B) = P(A) P(B) The probability that all outcomes with be favorable is the product of probablities of each event o ...
... The probability that there will be at least on successful outcome is the sum probability of the first event and second event occurring minus the probablity that both will occur P(A and B) = P(A) P(B) The probability that all outcomes with be favorable is the product of probablities of each event o ...
Lecture 4
... The probability of an uncertain event happening is the “degree of belief” in the event held by the individual given their experience and information. 2. Objective or frequentist probability The chance of something gives the percentage of the time it is expected to happen when the process is done ove ...
... The probability of an uncertain event happening is the “degree of belief” in the event held by the individual given their experience and information. 2. Objective or frequentist probability The chance of something gives the percentage of the time it is expected to happen when the process is done ove ...
Compound Probability March 10, 2014
... 6. In the Seattle Mariners’ historical 2001 season, Edgar Martinez batted 0.306 (meaning 30.6% of the times he was at the plate he got a hit), Ichiro Suzuki batted 0.350, and Bret Boone batted 0.331. If these three players were to each come up to bat one more time, what is the probability that none ...
... 6. In the Seattle Mariners’ historical 2001 season, Edgar Martinez batted 0.306 (meaning 30.6% of the times he was at the plate he got a hit), Ichiro Suzuki batted 0.350, and Bret Boone batted 0.331. If these three players were to each come up to bat one more time, what is the probability that none ...
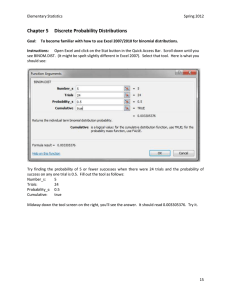
Chapter 5 Discrete Probability Distributions
... being hired is 0.001, quite a bit less than 0.05. Therefore, we can conclude that it is most likely that the original assumption was incorrect, i.e. it is far more likely that a hiring bias based on gender did exist. This is an important and powerful application of the binomial distribution. Please ...
... being hired is 0.001, quite a bit less than 0.05. Therefore, we can conclude that it is most likely that the original assumption was incorrect, i.e. it is far more likely that a hiring bias based on gender did exist. This is an important and powerful application of the binomial distribution. Please ...
1.5 Backward Kolmogorov equation
... depends on the initial composition of the population that we shall denote by 0 < y < 1, i.e. p(x, t = 0) = δ(x − y). Starting from this initial condition, we can follow the probability distribution p(x, t) via the forward Kolmogorov equation (1.42). For purposes of finding the long-time behavior wit ...
... depends on the initial composition of the population that we shall denote by 0 < y < 1, i.e. p(x, t = 0) = δ(x − y). Starting from this initial condition, we can follow the probability distribution p(x, t) via the forward Kolmogorov equation (1.42). For purposes of finding the long-time behavior wit ...
Chapter 11 Notes
... Ex. 7 A survey showed that 47 % of students worked during the summer. Of those who worked, 62 % watched 2 hours or more of TV per day. Those who didn’t work, 79 % watched 2 or more hours of TV. What is the probability that you choose a random student who watched fewer than 2 hours of TV per day. ...
... Ex. 7 A survey showed that 47 % of students worked during the summer. Of those who worked, 62 % watched 2 hours or more of TV per day. Those who didn’t work, 79 % watched 2 or more hours of TV. What is the probability that you choose a random student who watched fewer than 2 hours of TV per day. ...
Conditional probability
... The prosecutor drew a grid with 1cm spacing on the paper, and showed that there were 4 cases of one sequence of syllables aligning up. The prosecutors case was that the probability of even a single alignment was tiny (to make up for my memory lapse, let us just say it is .1). Therefore, the prosecu ...
... The prosecutor drew a grid with 1cm spacing on the paper, and showed that there were 4 cases of one sequence of syllables aligning up. The prosecutors case was that the probability of even a single alignment was tiny (to make up for my memory lapse, let us just say it is .1). Therefore, the prosecu ...
Math 1312 – Test II review
... members), College of Business( 60 members), College of Professional Studies(100), and College of Liberal Arts(60). How many different groups of four can be selected ? ...
... members), College of Business( 60 members), College of Professional Studies(100), and College of Liberal Arts(60). How many different groups of four can be selected ? ...
Binomial Random Variable
... 4.Are the trials independent? Yes, since each individual does their mazes separately. There is some reason for concern that the third condition is violated. However, since we can go ahead and assume that the probability, p, of success is the same for each individual. With that assumptions made, then ...
... 4.Are the trials independent? Yes, since each individual does their mazes separately. There is some reason for concern that the third condition is violated. However, since we can go ahead and assume that the probability, p, of success is the same for each individual. With that assumptions made, then ...
CPSC 1820 Assignment 4 Solutions
... move made on the path, and so on. We must count the total number of possible strings of 3 Xs, 5 Ys and 4 Zs. Each string will contain 3 + 5 + 4 = 12 letters where the 3 Xs are indistinguishable ...
... move made on the path, and so on. We must count the total number of possible strings of 3 Xs, 5 Ys and 4 Zs. Each string will contain 3 + 5 + 4 = 12 letters where the 3 Xs are indistinguishable ...
Level 1 Mathematics, 2009 - SMC-Math
... 5% of Sarah’s DVDs that are less than two hours in length are scratched. Sarah owns 258 DVDs. How many of her DVDs that are less than 2 hours in length would you expect to be a comedy and scratched? Use probabilities and/or diagrams to explain and support your answer. ...
... 5% of Sarah’s DVDs that are less than two hours in length are scratched. Sarah owns 258 DVDs. How many of her DVDs that are less than 2 hours in length would you expect to be a comedy and scratched? Use probabilities and/or diagrams to explain and support your answer. ...
Infinite monkey theorem

The infinite monkey theorem states that a monkey hitting keys at random on a typewriter keyboard for an infinite amount of time will almost surely type a given text, such as the complete works of William Shakespeare.In this context, ""almost surely"" is a mathematical term with a precise meaning, and the ""monkey"" is not an actual monkey, but a metaphor for an abstract device that produces an endless random sequence of letters and symbols. One of the earliest instances of the use of the ""monkey metaphor"" is that of French mathematician Émile Borel in 1913, but the first instance may be even earlier. The relevance of the theorem is questionable—the probability of a universe full of monkeys typing a complete work such as Shakespeare's Hamlet is so tiny that the chance of it occurring during a period of time hundreds of thousands of orders of magnitude longer than the age of the universe is extremely low (but technically not zero). It should also be noted that real monkeys don't produce uniformly random output, which means that an actual monkey hitting keys for an infinite amount of time has no statistical certainty of ever producing any given text.Variants of the theorem include multiple and even infinitely many typists, and the target text varies between an entire library and a single sentence. The history of these statements can be traced back to Aristotle's On Generation and Corruption and Cicero's De natura deorum (On the Nature of the Gods), through Blaise Pascal and Jonathan Swift, and finally to modern statements with their iconic simians and typewriters. In the early 20th century, Émile Borel and Arthur Eddington used the theorem to illustrate the timescales implicit in the foundations of statistical mechanics.