CS214 * Data Structures Lecture 01: A Course Overview
... 3) Definiteness – Each instruction is clear and unambiguous. 4) Finiteness – If we trace out the instructions of an algorithm, then for all cases, the algorithm terminates after a finite number of steps. 5) Efficiency – The algorithm must consume a reasonable amount of resources and takes a reasonab ...
... 3) Definiteness – Each instruction is clear and unambiguous. 4) Finiteness – If we trace out the instructions of an algorithm, then for all cases, the algorithm terminates after a finite number of steps. 5) Efficiency – The algorithm must consume a reasonable amount of resources and takes a reasonab ...
Midterm I Solutions - Bakersfield College
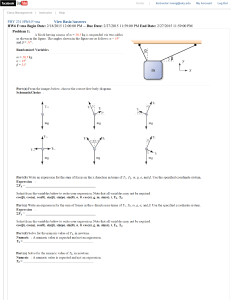
... 10. Find the area of the given triangle (the angle is in radians). Round off your answer to the nearest hundredth. This triangle isn't really a valid one; there are two approaches, that yield different answers. Either answer was marked as correct. Solution 1: Using the fact that a right triangle has ...
... 10. Find the area of the given triangle (the angle is in radians). Round off your answer to the nearest hundredth. This triangle isn't really a valid one; there are two approaches, that yield different answers. Either answer was marked as correct. Solution 1: Using the fact that a right triangle has ...
A Quick Overview of Computational Complexity
... •When do we say that a program has polynomial complexity •What does it mean that a problem is P?, in NP? •What does it mean that a problem is NP-complete? ...
... •When do we say that a program has polynomial complexity •What does it mean that a problem is P?, in NP? •What does it mean that a problem is NP-complete? ...
K-Lines: A theory of memory – Marvin Minsky
... Marr’s view of the paper… What Minsky does in this paper, is define a scenario via which the brain takes a Type 2 problem approach to solving it. Without requiring an underlying principle to the solution or such, the basic idea is to look for similar problems that have been encountered in the past. ...
... Marr’s view of the paper… What Minsky does in this paper, is define a scenario via which the brain takes a Type 2 problem approach to solving it. Without requiring an underlying principle to the solution or such, the basic idea is to look for similar problems that have been encountered in the past. ...
ComputationalComplex.. - Computer Science & Engineering
... in polynomial time by nondeterministic computers NP Include all problems in P The key question is are there problems in NP that are not in P or is P = NP? We don’t know the answer to the previous question But there are a particular kind of problems, the NP-complete problems, for which all known dete ...
... in polynomial time by nondeterministic computers NP Include all problems in P The key question is are there problems in NP that are not in P or is P = NP? We don’t know the answer to the previous question But there are a particular kind of problems, the NP-complete problems, for which all known dete ...
Q 5.2 : Consider the rough guide to worst
... representation of elevation field defined over the USA. For simplicity, use square based tesselation of a Euclidean plane. Assume the availability of a geo-coding service to convert POI to grid row and column. For simplicity, focus on non-nested tessellations. ...
... representation of elevation field defined over the USA. For simplicity, use square based tesselation of a Euclidean plane. Assume the availability of a geo-coding service to convert POI to grid row and column. For simplicity, focus on non-nested tessellations. ...
Senior Member, IEEE
... • During these operations, the basic problem characteristics are abstracted into a schema • Theorem 2: Under the immune selection, if the vaccination makes the fitness of an individual higher than the average fitness of the current population, then the schema of the corresponding vaccine will be dif ...
... • During these operations, the basic problem characteristics are abstracted into a schema • Theorem 2: Under the immune selection, if the vaccination makes the fitness of an individual higher than the average fitness of the current population, then the schema of the corresponding vaccine will be dif ...
Travelling salesman problem
The travelling salesman problem (TSP) asks the following question: Given a list of cities and the distances between each pair of cities, what is the shortest possible route that visits each city exactly once and returns to the origin city? It is an NP-hard problem in combinatorial optimization, important in operations research and theoretical computer science.TSP is a special case of the travelling purchaser problem and the Vehicle routing problem.In the theory of computational complexity, the decision version of the TSP (where, given a length L, the task is to decide whether the graph has any tour shorter than L) belongs to the class of NP-complete problems. Thus, it is possible that the worst-case running time for any algorithm for the TSP increases superpolynomially (perhaps, specifically, exponentially) with the number of cities.The problem was first formulated in 1930 and is one of the most intensively studied problems in optimization. It is used as a benchmark for many optimization methods. Even though the problem is computationally difficult, a large number of heuristics and exact methods are known, so that some instances with tens of thousands of cities can be solved completely and even problems with millions of cities can be approximated within a small fraction of 1%.The TSP has several applications even in its purest formulation, such as planning, logistics, and the manufacture of microchips. Slightly modified, it appears as a sub-problem in many areas, such as DNA sequencing. In these applications, the concept city represents, for example, customers, soldering points, or DNA fragments, and the concept distance represents travelling times or cost, or a similarity measure between DNA fragments. The TSP also appears in astronomy, as astronomers observing many sources will want to minimise the time spent slewing the telescope between the sources. In many applications, additional constraints such as limited resources or time windows may be imposed.