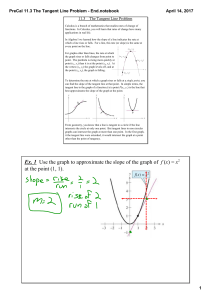
Lecture notes for Section 3.4
... Big Idea: Sometimes you want to graph the situation where the outcome of a calculation involving two variables is greater than or less than a given number. For those cases, we need to learn how to graph linear inequalities in two variables to represent all the possible solutions. Big Skill: You shou ...
... Big Idea: Sometimes you want to graph the situation where the outcome of a calculation involving two variables is greater than or less than a given number. For those cases, we need to learn how to graph linear inequalities in two variables to represent all the possible solutions. Big Skill: You shou ...
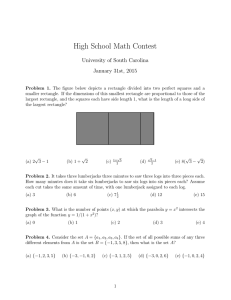
High School Math Contest University of South Carolina January 31st, 2015
... Problem 30. Four prisoners are numbered 1 through 4. They are informed by the jail warden that each of them, in turn, will be taken to a room with four boxes labeled 1 through 4. The numbers 1 through 4 are written on four slips of paper, one number per slip. These slips are placed into the boxes a ...
... Problem 30. Four prisoners are numbered 1 through 4. They are informed by the jail warden that each of them, in turn, will be taken to a room with four boxes labeled 1 through 4. The numbers 1 through 4 are written on four slips of paper, one number per slip. These slips are placed into the boxes a ...
open pdf file
... the number of both be positive trick skis and y represent the number of slalom skis. Then the Number of following system of linear trick skis has inequalities describes our to be less than problem mathematically. or equal to 15 Actually, only whole numbers Constraint on for x and y should be used, b ...
... the number of both be positive trick skis and y represent the number of slalom skis. Then the Number of following system of linear trick skis has inequalities describes our to be less than problem mathematically. or equal to 15 Actually, only whole numbers Constraint on for x and y should be used, b ...
Chapter 11 - Data Collections
... Lists in Python are heterogeneous, which means they can hold multiple types of values at once. Problem 4: A python list cannot grow or shrink in size Solution False This is often true in other languages. In Python, lists are dynamic and grow and shrink as needed. Problem 5: Unlike strings, Python li ...
... Lists in Python are heterogeneous, which means they can hold multiple types of values at once. Problem 4: A python list cannot grow or shrink in size Solution False This is often true in other languages. In Python, lists are dynamic and grow and shrink as needed. Problem 5: Unlike strings, Python li ...
Swarm_Intelligence-prakhar
... computing behaviour is governed by same set of rules.) the interactions among the individuals are based on simple behavioral rules that exploit only local information that the individuals exchange directly or via the environment the overall behaviour of the system results from the interactions of in ...
... computing behaviour is governed by same set of rules.) the interactions among the individuals are based on simple behavioral rules that exploit only local information that the individuals exchange directly or via the environment the overall behaviour of the system results from the interactions of in ...
Travelling salesman problem
The travelling salesman problem (TSP) asks the following question: Given a list of cities and the distances between each pair of cities, what is the shortest possible route that visits each city exactly once and returns to the origin city? It is an NP-hard problem in combinatorial optimization, important in operations research and theoretical computer science.TSP is a special case of the travelling purchaser problem and the Vehicle routing problem.In the theory of computational complexity, the decision version of the TSP (where, given a length L, the task is to decide whether the graph has any tour shorter than L) belongs to the class of NP-complete problems. Thus, it is possible that the worst-case running time for any algorithm for the TSP increases superpolynomially (perhaps, specifically, exponentially) with the number of cities.The problem was first formulated in 1930 and is one of the most intensively studied problems in optimization. It is used as a benchmark for many optimization methods. Even though the problem is computationally difficult, a large number of heuristics and exact methods are known, so that some instances with tens of thousands of cities can be solved completely and even problems with millions of cities can be approximated within a small fraction of 1%.The TSP has several applications even in its purest formulation, such as planning, logistics, and the manufacture of microchips. Slightly modified, it appears as a sub-problem in many areas, such as DNA sequencing. In these applications, the concept city represents, for example, customers, soldering points, or DNA fragments, and the concept distance represents travelling times or cost, or a similarity measure between DNA fragments. The TSP also appears in astronomy, as astronomers observing many sources will want to minimise the time spent slewing the telescope between the sources. In many applications, additional constraints such as limited resources or time windows may be imposed.