Introduction to higher homotopy groups and
... for any two points x0 , x1 ∈ X. Moreover, if X is simply connected, then this isomorphism is canonical, and so πk (X) is a well-defined group without the choice of a base point. If X is not simply connected, then the isomorphism (3.1) might not be canonical. In particular, for a noncontractible loop ...
... for any two points x0 , x1 ∈ X. Moreover, if X is simply connected, then this isomorphism is canonical, and so πk (X) is a well-defined group without the choice of a base point. If X is not simply connected, then the isomorphism (3.1) might not be canonical. In particular, for a noncontractible loop ...
An Introduction to Computational Group Theory
... solution of the word problem, Find an algorithm to decide whether, in a group defined by a finite set of abstract generators and relators, a word in the generators represents the identity. Dehn’s question was motivated by topological considerations; even today it is hard to draw a sharp border betwe ...
... solution of the word problem, Find an algorithm to decide whether, in a group defined by a finite set of abstract generators and relators, a word in the generators represents the identity. Dehn’s question was motivated by topological considerations; even today it is hard to draw a sharp border betwe ...
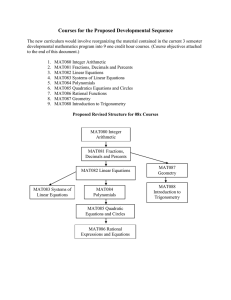
Courses for the Proposed Developmental Sequence
... Solve quadratic equations by factoring and the square root property. Intermediate Algebra, Section 8.1 Solve quadratic equations by completing the square. Intermediate Algebra, Section 8.2 Solve quadratic equations by using the quadratic formula. Intermediate Algebra, Section 8.3 Find the vertex and ...
... Solve quadratic equations by factoring and the square root property. Intermediate Algebra, Section 8.1 Solve quadratic equations by completing the square. Intermediate Algebra, Section 8.2 Solve quadratic equations by using the quadratic formula. Intermediate Algebra, Section 8.3 Find the vertex and ...
Flatness
... Proposition 1.1 The A-module M is flat iff Tor1 (M, N ) = 0 for every A-module N . Using the LES of Tor, this immediately implies: Proposition 1.2 If 0 → M 0 → M → M 00 → 0 is an exact sequence of A-modules, and M 0 and M 00 are flat, then so is M . If M and M 00 are both flat, so is M 0 . Another ...
... Proposition 1.1 The A-module M is flat iff Tor1 (M, N ) = 0 for every A-module N . Using the LES of Tor, this immediately implies: Proposition 1.2 If 0 → M 0 → M → M 00 → 0 is an exact sequence of A-modules, and M 0 and M 00 are flat, then so is M . If M and M 00 are both flat, so is M 0 . Another ...
A. Case Structures
... To select a case, type the values in the case selector identifier or use the Labeling tool to edit the values. Specify a single value or lists and ranges of values to select the case. For lists, use commas to separate values. Specify a range as 10..20, meaning all numbers from 10 to 20 inclusively. ...
... To select a case, type the values in the case selector identifier or use the Labeling tool to edit the values. Specify a single value or lists and ranges of values to select the case. For lists, use commas to separate values. Specify a range as 10..20, meaning all numbers from 10 to 20 inclusively. ...
Complexity of intersection of real quadrics and topology of
... introduced by A. A. Agrachev in [1] and developed by him and the author in [3]. The powerful of this bounds is that they are intrinsic and different X might produce different ones: for example a set W whose nonzero forms have constant rank has base locus with complexity bounded by b(RPn ). On the ot ...
... introduced by A. A. Agrachev in [1] and developed by him and the author in [3]. The powerful of this bounds is that they are intrinsic and different X might produce different ones: for example a set W whose nonzero forms have constant rank has base locus with complexity bounded by b(RPn ). On the ot ...
Modular forms and differential operators
... are again modular forms, and in 1977, H Cohen defined for each n i> 0 a bilinear operation which assigns to two modular forms f and g of weight k and l a modular form If, g], of weight k + l + 2n. In the present paper we study these "Rankin-Cohen brackets" from t w o points of view. On the one hand ...
... are again modular forms, and in 1977, H Cohen defined for each n i> 0 a bilinear operation which assigns to two modular forms f and g of weight k and l a modular form If, g], of weight k + l + 2n. In the present paper we study these "Rankin-Cohen brackets" from t w o points of view. On the one hand ...
SOME NOTES ON RECENT WORK OF DANI WISE
... (6) J has a relatively simple, understandable structure. One should apply this scheme when G is a 3-manifold groups, one-relator groups, HNN extensions of free groups by cyclic subgroups, matrix groups, etc., to obtain and study various properties which may not be algebraically available. Namely, on ...
... (6) J has a relatively simple, understandable structure. One should apply this scheme when G is a 3-manifold groups, one-relator groups, HNN extensions of free groups by cyclic subgroups, matrix groups, etc., to obtain and study various properties which may not be algebraically available. Namely, on ...
On Idempotent Measures of Small Norm
... Furthermore, for any open set of the form Uε,K2 , there is some open Uε,K1 such that ι(Uε,K1 ) = Uε,K2 , hence ι is a homeomorphism, thus it is a homeomorphic isomorphism [ to Λ. from G/H d is isomorphic to H, and so by the Pontryagin As H and Λ are mutual annihilators, Γ/Λ b and the theorem is prov ...
... Furthermore, for any open set of the form Uε,K2 , there is some open Uε,K1 such that ι(Uε,K1 ) = Uε,K2 , hence ι is a homeomorphism, thus it is a homeomorphic isomorphism [ to Λ. from G/H d is isomorphic to H, and so by the Pontryagin As H and Λ are mutual annihilators, Γ/Λ b and the theorem is prov ...
Some applications of the ultrafilter topology on spaces of valuation
... B{x} of Z. This topology is now called the Zariski topology on Z and the set Z, equipped with this topology, denoted also by Z zar , is usually called the (abstract) Zariski-Riemann surface of K over A. Zariski proved the quasi-compactness of Z zar and later it was proven and rediscovered by several ...
... B{x} of Z. This topology is now called the Zariski topology on Z and the set Z, equipped with this topology, denoted also by Z zar , is usually called the (abstract) Zariski-Riemann surface of K over A. Zariski proved the quasi-compactness of Z zar and later it was proven and rediscovered by several ...
Full Groups of Equivalence Relations
... and therefore Polish. It also has a two-sided invariant metric. ...
... and therefore Polish. It also has a two-sided invariant metric. ...
Homological algebra

Homological algebra is the branch of mathematics that studies homology in a general algebraic setting. It is a relatively young discipline, whose origins can be traced to investigations in combinatorial topology (a precursor to algebraic topology) and abstract algebra (theory of modules and syzygies) at the end of the 19th century, chiefly by Henri Poincaré and David Hilbert. The development of homological algebra was closely intertwined with the emergence of category theory. By and large, homological algebra is the study of homological functors and the intricate algebraic structures that they entail. One quite useful and ubiquitous concept in mathematics is that of chain complexes, which can be studied both through their homology and cohomology. Homological algebra affords the means to extract information contained in these complexes and present it in the form of homological invariants of rings, modules, topological spaces, and other 'tangible' mathematical objects. A powerful tool for doing this is provided by spectral sequences.From its very origins, homological algebra has played an enormous role in algebraic topology. Its sphere of influence has gradually expanded and presently includes commutative algebra, algebraic geometry, algebraic number theory, representation theory, mathematical physics, operator algebras, complex analysis, and the theory of partial differential equations. K-theory is an independent discipline which draws upon methods of homological algebra, as does the noncommutative geometry of Alain Connes.