Affine Varieties
... Thus the maps Φ = (f 1 , ..., f m ) : X → Y are in a natural bijection with the C-algebra homomorphisms Φ∗ : C[Y ] → C[X], since any such Φ is clearly a regular map. Remark: If we think of the affine varieties (with sheaves of regular functions) as a category with regular maps as the morphisms, then ...
... Thus the maps Φ = (f 1 , ..., f m ) : X → Y are in a natural bijection with the C-algebra homomorphisms Φ∗ : C[Y ] → C[X], since any such Φ is clearly a regular map. Remark: If we think of the affine varieties (with sheaves of regular functions) as a category with regular maps as the morphisms, then ...
alg6.1
... 6-1 Integer Exponents Check It Out! Example 3b Evaluate the expression for the given values of the variables. for a = –2 and b = 6 Substitute –2 for a and 6 for b. Simplify expressions with exponents. Write the power in the denominator as a product. Simplify the denominator. ...
... 6-1 Integer Exponents Check It Out! Example 3b Evaluate the expression for the given values of the variables. for a = –2 and b = 6 Substitute –2 for a and 6 for b. Simplify expressions with exponents. Write the power in the denominator as a product. Simplify the denominator. ...
A model structure for quasi-categories
... model for the “homotopy theory of homotopy theories.” In some sense a “homotopy theory” can be regarded as a category with some class of weak equivalences that one would like to formally invert. Any such homotopy theory gives rise to a simplicial category, and conversely simplicial categories arise ...
... model for the “homotopy theory of homotopy theories.” In some sense a “homotopy theory” can be regarded as a category with some class of weak equivalences that one would like to formally invert. Any such homotopy theory gives rise to a simplicial category, and conversely simplicial categories arise ...
Uniformities and uniformly continuous functions on locally
... specimen of a topological group that is not SIN. (See [3, 8].) An obvious corollary of the SIN property is that every left uniformly continuous real-valued function on G is right uniformly continuous (and vice versa). Rather surprisingly, it is still unknown if the converse holds true. OPEN QUESTION ...
... specimen of a topological group that is not SIN. (See [3, 8].) An obvious corollary of the SIN property is that every left uniformly continuous real-valued function on G is right uniformly continuous (and vice versa). Rather surprisingly, it is still unknown if the converse holds true. OPEN QUESTION ...
Note on Nakayama`s Lemma For Compact Λ
... We now consider the stronger version of Nakayama’s lemma. Let I = Ker(Λ(G) → Zp ) be the augmentation ideal of Λ = Λ(G). It is well known that, in the case of G = Zp and with X as above, if X/IX is finite then X is actually a torsion Λ module. This is immediate from the structure theorem for Λ modul ...
... We now consider the stronger version of Nakayama’s lemma. Let I = Ker(Λ(G) → Zp ) be the augmentation ideal of Λ = Λ(G). It is well known that, in the case of G = Zp and with X as above, if X/IX is finite then X is actually a torsion Λ module. This is immediate from the structure theorem for Λ modul ...
10 Rings
... If we additionally have 0 6= 1 and, we can divide by any non-zero element, i.e., (x) for each a 6= 0 ∈ R, there exists a−1 such that aa−1 = 1, then we say R is a field. Note that if all the properties and (a) and (b) hold except for (vi)1 , we say R is a noncommutative ring. We will primarily be int ...
... If we additionally have 0 6= 1 and, we can divide by any non-zero element, i.e., (x) for each a 6= 0 ∈ R, there exists a−1 such that aa−1 = 1, then we say R is a field. Note that if all the properties and (a) and (b) hold except for (vi)1 , we say R is a noncommutative ring. We will primarily be int ...
GROUP THEORY 1. Groups A set G is called a group if there is a
... central elements is called the center of G. Let H ⊆ G be a subgroup. Define the normalizer NH of H as {g ∈ G| gHg −1 ⊆ H}. This is the smallest subgroup of G, in which H is normal. If S ⊆ G is an arbitrary subset, then define the centralizer ZS of S as {g ∈ G | (∀x ∈ S) gx = xg}. This is the smalles ...
... central elements is called the center of G. Let H ⊆ G be a subgroup. Define the normalizer NH of H as {g ∈ G| gHg −1 ⊆ H}. This is the smallest subgroup of G, in which H is normal. If S ⊆ G is an arbitrary subset, then define the centralizer ZS of S as {g ∈ G | (∀x ∈ S) gx = xg}. This is the smalles ...
Math 3121 Lecture 11
... – Theorem: The image of a group homomorphism is isomorphic to the group modulo its kernel. – Properties of normal subgroups – Theorem: For a subgroup of a group, left coset multiplication is welldefined if and only if the subgroup is normal. – Theorem: The canonical map is a homomorphism. ...
... – Theorem: The image of a group homomorphism is isomorphic to the group modulo its kernel. – Properties of normal subgroups – Theorem: For a subgroup of a group, left coset multiplication is welldefined if and only if the subgroup is normal. – Theorem: The canonical map is a homomorphism. ...
Lie Theory Through Examples
... In this class we’ll talk about a classic subject: the theory of simple Lie groups and simple Lie algebras. This theory ties together some of the most beautiful, symmetrical structures in mathematics: Platonic solids and their higher-dimensional cousins, finite groups generated by reflections, lattic ...
... In this class we’ll talk about a classic subject: the theory of simple Lie groups and simple Lie algebras. This theory ties together some of the most beautiful, symmetrical structures in mathematics: Platonic solids and their higher-dimensional cousins, finite groups generated by reflections, lattic ...
Homotopy Theory of Topological Spaces and Simplicial Sets
... and if f g = ida and gf = idb we will call the objects a and b isomorphic, as usual. Isomorphic objects will have some common properties, depending on the category. For example in the setting of sets as before isomorphisms are just bijections and the sets that are isomorphic will have the same cardi ...
... and if f g = ida and gf = idb we will call the objects a and b isomorphic, as usual. Isomorphic objects will have some common properties, depending on the category. For example in the setting of sets as before isomorphisms are just bijections and the sets that are isomorphic will have the same cardi ...
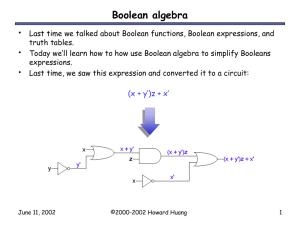
Boolean Algebra
... Any Boolean expression can be implemented with a circuit, which uses primitive logic gates to compute products, sums and complements. We saw two ways to prove equivalence of expressions: – Truth tables show that all possible inputs yield the same results. – Boolean algebra is especially useful for s ...
... Any Boolean expression can be implemented with a circuit, which uses primitive logic gates to compute products, sums and complements. We saw two ways to prove equivalence of expressions: – Truth tables show that all possible inputs yield the same results. – Boolean algebra is especially useful for s ...
Homological algebra

Homological algebra is the branch of mathematics that studies homology in a general algebraic setting. It is a relatively young discipline, whose origins can be traced to investigations in combinatorial topology (a precursor to algebraic topology) and abstract algebra (theory of modules and syzygies) at the end of the 19th century, chiefly by Henri Poincaré and David Hilbert. The development of homological algebra was closely intertwined with the emergence of category theory. By and large, homological algebra is the study of homological functors and the intricate algebraic structures that they entail. One quite useful and ubiquitous concept in mathematics is that of chain complexes, which can be studied both through their homology and cohomology. Homological algebra affords the means to extract information contained in these complexes and present it in the form of homological invariants of rings, modules, topological spaces, and other 'tangible' mathematical objects. A powerful tool for doing this is provided by spectral sequences.From its very origins, homological algebra has played an enormous role in algebraic topology. Its sphere of influence has gradually expanded and presently includes commutative algebra, algebraic geometry, algebraic number theory, representation theory, mathematical physics, operator algebras, complex analysis, and the theory of partial differential equations. K-theory is an independent discipline which draws upon methods of homological algebra, as does the noncommutative geometry of Alain Connes.