Computing the square roots of matrices with central symmetry 1
... the real case. The method first computes the Schur decomposition A = U T U H , where U is unitary and T is upper triangular; then finds S, upper triangular, such that S 2 = T , using a fast recursion (viz., Parlett recurrence [22, 23]); finally, computes X = U SU H , which is the desired square root ...
... the real case. The method first computes the Schur decomposition A = U T U H , where U is unitary and T is upper triangular; then finds S, upper triangular, such that S 2 = T , using a fast recursion (viz., Parlett recurrence [22, 23]); finally, computes X = U SU H , which is the desired square root ...
Randomized algorithms for matrices and massive datasets
... • To approximate a matrix A, keep a few elements of the matrix (instead of rows or columns) and zero out the remaining elements. • Compute a rank k approximation to this sparse matrix (using Lanczos methods). ...
... • To approximate a matrix A, keep a few elements of the matrix (instead of rows or columns) and zero out the remaining elements. • Compute a rank k approximation to this sparse matrix (using Lanczos methods). ...
Faculty of Engineering - Multimedia University
... Step 6: To run the m-file from the MATLAB Editor window, go to Tools -> Run. You can also execute the m-file from the Command Window by typing the m-file name (without the “.m”) on the command line. ...
... Step 6: To run the m-file from the MATLAB Editor window, go to Tools -> Run. You can also execute the m-file from the Command Window by typing the m-file name (without the “.m”) on the command line. ...
Non–singular matrix
... A is called non–singular or invertible if there exists an n × n matrix B such that AB = In = BA. Any matrix B with the above property is called an inverse of A. If A does not have an inverse, A is called singular. THEOREM. (Inverses are unique) If A has inverses B and C, then B = C. If A has an inve ...
... A is called non–singular or invertible if there exists an n × n matrix B such that AB = In = BA. Any matrix B with the above property is called an inverse of A. If A does not have an inverse, A is called singular. THEOREM. (Inverses are unique) If A has inverses B and C, then B = C. If A has an inve ...
Lower Bounds on Matrix Rigidity via a Quantum
... Very briefly, an r-dimensional quantum state is a unit vector of complex ampliPr tudes, written |φi = i=1 αi |ii ∈ Cr . Here |ii is the r-dimensional vector that has a 1 in P its ith coordinate andP0s elsewhere. The inner product between |φi and |ψi = ri=1 βi |ii is hφ|ψi = i α∗i βi . A measurement ...
... Very briefly, an r-dimensional quantum state is a unit vector of complex ampliPr tudes, written |φi = i=1 αi |ii ∈ Cr . Here |ii is the r-dimensional vector that has a 1 in P its ith coordinate andP0s elsewhere. The inner product between |φi and |ψi = ri=1 βi |ii is hφ|ψi = i α∗i βi . A measurement ...
Linear Transformations and Matrices
... Proof All that remains is to verify axioms (R7) and (R8) for a ring as given in Section 1.4. This is quite easy to do, and we leave it to the reader (see Exercise 5.2.1). ˙ In fact, it is easy to see that L(V) is a ring with unit element. In particular, we define the identity mapping I ∞ L(V) by I(x ...
... Proof All that remains is to verify axioms (R7) and (R8) for a ring as given in Section 1.4. This is quite easy to do, and we leave it to the reader (see Exercise 5.2.1). ˙ In fact, it is easy to see that L(V) is a ring with unit element. In particular, we define the identity mapping I ∞ L(V) by I(x ...
Chapter 1 Linear Algebra
... S1 If v and w are vectors in W, then so is v + w; and S2 For any scalar λ ∈ R, if w is any vector in W, then so is λ w. If these two properties are satisfied we say that W is a vector subspace of V. One also often sees the phrases ‘W is a subspace of V’ and ‘W is a linear subspace of V.’ Let us make ...
... S1 If v and w are vectors in W, then so is v + w; and S2 For any scalar λ ∈ R, if w is any vector in W, then so is λ w. If these two properties are satisfied we say that W is a vector subspace of V. One also often sees the phrases ‘W is a subspace of V’ and ‘W is a linear subspace of V.’ Let us make ...
Projection (linear algebra)
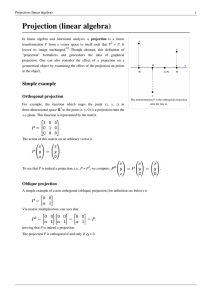
... assemble these vectors in the matrix B. Then the projection is defined by This expression generalizes the formula for orthogonal projections given above.[7] ...
... assemble these vectors in the matrix B. Then the projection is defined by This expression generalizes the formula for orthogonal projections given above.[7] ...
Jordan normal form
In linear algebra, a Jordan normal form (often called Jordan canonical form)of a linear operator on a finite-dimensional vector space is an upper triangular matrix of a particular form called a Jordan matrix, representing the operator with respect to some basis. Such matrix has each non-zero off-diagonal entry equal to 1, immediately above the main diagonal (on the superdiagonal), and with identical diagonal entries to the left and below them. If the vector space is over a field K, then a basis with respect to which the matrix has the required form exists if and only if all eigenvalues of the matrix lie in K, or equivalently if the characteristic polynomial of the operator splits into linear factors over K. This condition is always satisfied if K is the field of complex numbers. The diagonal entries of the normal form are the eigenvalues of the operator, with the number of times each one occurs being given by its algebraic multiplicity.If the operator is originally given by a square matrix M, then its Jordan normal form is also called the Jordan normal form of M. Any square matrix has a Jordan normal form if the field of coefficients is extended to one containing all the eigenvalues of the matrix. In spite of its name, the normal form for a given M is not entirely unique, as it is a block diagonal matrix formed of Jordan blocks, the order of which is not fixed; it is conventional to group blocks for the same eigenvalue together, but no ordering is imposed among the eigenvalues, nor among the blocks for a given eigenvalue, although the latter could for instance be ordered by weakly decreasing size.The Jordan–Chevalley decomposition is particularly simple with respect to a basis for which the operator takes its Jordan normal form. The diagonal form for diagonalizable matrices, for instance normal matrices, is a special case of the Jordan normal form.The Jordan normal form is named after Camille Jordan.