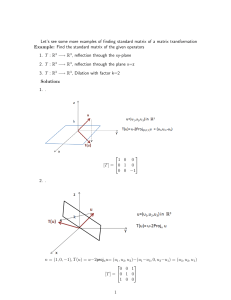
Find the standard matrix of the gi
... One-to-one Matrix Transformations and Inverse of a one-to-one Matrix Operator To be able to define inverse of a matrix transformation we need to have one-to-one matrix operator Definition: A matrix transformation T : Rn → Rm is said to be one-to-one if T maps distinct vectors (points) in Rn into dis ...
... One-to-one Matrix Transformations and Inverse of a one-to-one Matrix Operator To be able to define inverse of a matrix transformation we need to have one-to-one matrix operator Definition: A matrix transformation T : Rn → Rm is said to be one-to-one if T maps distinct vectors (points) in Rn into dis ...
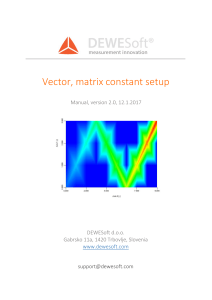
Vector, matrix constant
... Basically, all operations should work on arrays, but there are some limitations to it. We can for example do the following formula, where all elements in the array will be subtracted. ...
... Basically, all operations should work on arrays, but there are some limitations to it. We can for example do the following formula, where all elements in the array will be subtracted. ...
PDF
... Show that A cannot be invertible. (Hint: suppose it is: what does that tell you about B ?) If A has an inverse A−1 , then A−1 A = In , the n × n identity matrix. But then B = In B = (A−1 A)B = A−1 (AB) = A−1 O = O, the last because multiplying a row by a column of 0s gives 0. So if A is invertible, ...
... Show that A cannot be invertible. (Hint: suppose it is: what does that tell you about B ?) If A has an inverse A−1 , then A−1 A = In , the n × n identity matrix. But then B = In B = (A−1 A)B = A−1 (AB) = A−1 O = O, the last because multiplying a row by a column of 0s gives 0. So if A is invertible, ...
Show that when the unit vector j is multiplied by the following
... 7. (20 points) Draw appropriate free body diagrams (10 points) for the following problem from Chapter 3 of our textbook. Then answer the following True-False question, with a short explanation of your answer (10 points): “T or F: We can solve for the 3 unknown tensions and 1 unknown angle using Ga ...
... 7. (20 points) Draw appropriate free body diagrams (10 points) for the following problem from Chapter 3 of our textbook. Then answer the following True-False question, with a short explanation of your answer (10 points): “T or F: We can solve for the 3 unknown tensions and 1 unknown angle using Ga ...
A Brief Primer on Matrix Algebra
... Note that just as is the case for regular arithmetic (the technical term is “scalar algebra,” but that seems pretentious), the order in which matrices are added does not matter. Hence, A + B = B + A. Similarly, if both addition and subtraction are involved, the order of the operations does not matte ...
... Note that just as is the case for regular arithmetic (the technical term is “scalar algebra,” but that seems pretentious), the order in which matrices are added does not matter. Hence, A + B = B + A. Similarly, if both addition and subtraction are involved, the order of the operations does not matte ...
幻灯片 1
... The Zero matrix. The zero matrix is the matrix 0 all of those entries are 0. Idempotent matrices. A square matrix A is said to be idempotent iff A2 A Nilpotent matrices. A square matrix A is said to be nilpotent iff there is an integer q ...
... The Zero matrix. The zero matrix is the matrix 0 all of those entries are 0. Idempotent matrices. A square matrix A is said to be idempotent iff A2 A Nilpotent matrices. A square matrix A is said to be nilpotent iff there is an integer q ...
Non-negative matrix factorization

NMF redirects here. For the bridge convention, see new minor forcing.Non-negative matrix factorization (NMF), also non-negative matrix approximation is a group of algorithms in multivariate analysis and linear algebra where a matrix V is factorized into (usually) two matrices W and H, with the property that all three matrices have no negative elements. This non-negativity makes the resulting matrices easier to inspect. Also, in applications such as processing of audio spectrograms non-negativity is inherent to the data being considered. Since the problem is not exactly solvable in general, it is commonly approximated numerically.NMF finds applications in such fields as computer vision, document clustering, chemometrics, audio signal processing and recommender systems.