Review of Matrices and Vectors
... The following properties, which we give without proof, are essential background in the use of vectors and matrices in digital image processing. In each case, we assume a real matrix of order m×m although, as stated earlier, these results are equally applicable to complex numbers. 1. If {1, 2,…, q ...
... The following properties, which we give without proof, are essential background in the use of vectors and matrices in digital image processing. In each case, we assume a real matrix of order m×m although, as stated earlier, these results are equally applicable to complex numbers. 1. If {1, 2,…, q ...
Higher Order GSVD for Comparison of Global mRNA Expression
... science, accompanied by a need for mathematical frameworks that can compare multiple large-scale matrices with different row dimensions. The only such framework to date, the generalized singular value decomposition (GSVD), is limited to two matrices. We mathematically define a higher-order GSVD (HO ...
... science, accompanied by a need for mathematical frameworks that can compare multiple large-scale matrices with different row dimensions. The only such framework to date, the generalized singular value decomposition (GSVD), is limited to two matrices. We mathematically define a higher-order GSVD (HO ...
Simultaneous Analysis of Qualitative and Quantitative Data Analisi
... Followinq the works by Young (1981), Young, De Leeuw, ~ a k i n e 1 9 7 8 ) Tenenhaus ( 1977 ) this technique consists in transforminy each categorical variable into a numerical variable by allotting numerical scores to the cateqories. These scores are cptimally calculated in crder to get an optimal ...
... Followinq the works by Young (1981), Young, De Leeuw, ~ a k i n e 1 9 7 8 ) Tenenhaus ( 1977 ) this technique consists in transforminy each categorical variable into a numerical variable by allotting numerical scores to the cateqories. These scores are cptimally calculated in crder to get an optimal ...
EGR2013 Tutorial 8 Linear Algebra Outline Powers of a Matrix and
... A scalar is a quantity that is determined by its magnitude; A vector is a quantity that is determined by both its magnitude and its direction. Equality of Vectors: two vectors a and b are equal, if they have the same length and the same direction. Representations: in Cartesian coordinate system, the ...
... A scalar is a quantity that is determined by its magnitude; A vector is a quantity that is determined by both its magnitude and its direction. Equality of Vectors: two vectors a and b are equal, if they have the same length and the same direction. Representations: in Cartesian coordinate system, the ...
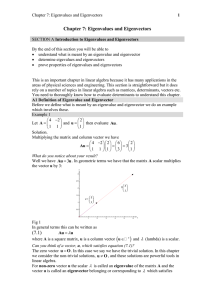
Chapter 7: Eigenvalues and Eigenvectors
... This is an important chapter in linear algebra because it has many applications in the areas of physical sciences and engineering. This section is straightforward but it does rely on a number of topics in linear algebra such as matrices, determinants, vectors etc. You need to thoroughly know how to ...
... This is an important chapter in linear algebra because it has many applications in the areas of physical sciences and engineering. This section is straightforward but it does rely on a number of topics in linear algebra such as matrices, determinants, vectors etc. You need to thoroughly know how to ...
A feasible BFGS-IP algorithm for solving
... ever, it is not uncommon to find situations where this requirement cannot be satisfied, in particular for large scale engineering problems (see [27] for an example, which partly motivates this study and deals with the estimation of parameters in a three phase flow in a porous medium). Despite the possi ...
... ever, it is not uncommon to find situations where this requirement cannot be satisfied, in particular for large scale engineering problems (see [27] for an example, which partly motivates this study and deals with the estimation of parameters in a three phase flow in a porous medium). Despite the possi ...
Non-negative matrix factorization

NMF redirects here. For the bridge convention, see new minor forcing.Non-negative matrix factorization (NMF), also non-negative matrix approximation is a group of algorithms in multivariate analysis and linear algebra where a matrix V is factorized into (usually) two matrices W and H, with the property that all three matrices have no negative elements. This non-negativity makes the resulting matrices easier to inspect. Also, in applications such as processing of audio spectrograms non-negativity is inherent to the data being considered. Since the problem is not exactly solvable in general, it is commonly approximated numerically.NMF finds applications in such fields as computer vision, document clustering, chemometrics, audio signal processing and recommender systems.