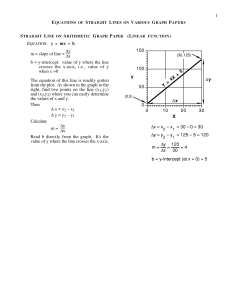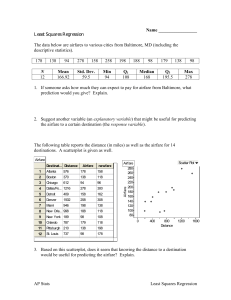
Elmer Models Manual
... The modular structure of the manual reflects the modular architecture of the software where new models may be written without any changes in the main program. Each solver has a separate section for theory and keywords, and often also some additional information is given, for example on the limitatio ...
... The modular structure of the manual reflects the modular architecture of the software where new models may be written without any changes in the main program. Each solver has a separate section for theory and keywords, and often also some additional information is given, for example on the limitatio ...
Washabaugh, A.P. and M. Zahn, A Chemical Reaction-based Boundary Condition for Flow Electrification, IEEE Transactions on Dielectrics and Electrical Insulation, Vol. 4, No. 6, pp. 688-709, December, 1997
... of the charged species that leads to the generation of the electrical double layer and it is the diffuse charge in the double layer that is transported by the fluid to accumulate or leak away at a downstream location. Unfortunately, since the ions responsible for the conduction in the liquid are usu ...
... of the charged species that leads to the generation of the electrical double layer and it is the diffuse charge in the double layer that is transported by the fluid to accumulate or leak away at a downstream location. Unfortunately, since the ions responsible for the conduction in the liquid are usu ...
... Many people believe the following: more work and more study results in higher grades. This is not necessarily so. You certainly must be willing to make a certain commitment of time and energy to this course, but the key to academic success is concentrating your efforts on the right things at the rig ...
Relativistic lagrangian non-linear field theories supporting non-topological soliton solutions UNIVERSIDAD DE OVIEDO
... soliton identity against a certain class of small perturbations for which the soliton configuration is a minimum of the energy functional. This restricted class of perturbations is defined through boundary conditions which amount, in general, to the preservation of (non-topological ) charges associa ...
... soliton identity against a certain class of small perturbations for which the soliton configuration is a minimum of the energy functional. This restricted class of perturbations is defined through boundary conditions which amount, in general, to the preservation of (non-topological ) charges associa ...
Partial differential equation

In mathematics, a partial differential equation (PDE) is a differential equation that contains unknown multivariable functions and their partial derivatives. (A special case are ordinary differential equations (ODEs), which deal with functions of a single variable and their derivatives.) PDEs are used to formulate problems involving functions of several variables, and are either solved by hand, or used to create a relevant computer model.PDEs can be used to describe a wide variety of phenomena such as sound, heat, electrostatics, electrodynamics, fluid flow, elasticity, or quantum mechanics. These seemingly distinct physical phenomena can be formalised similarly in terms of PDEs. Just as ordinary differential equations often model one-dimensional dynamical systems, partial differential equations often model multidimensional systems. PDEs find their generalisation in stochastic partial differential equations.