Zahn, M., Charge Injection and Transport in a Lossy Capacitor Stressed by a Marx Generator, IEEE Transactions on Electrical Insulation EI-19, 179-181, June 1984
... Approaching the x0=O, T=0 origin from along the axis has (x=0, 0-)=-, while approaching the origin from the t axis has E(x=0, t=0)=O for space charge limited conditions. This disgontinuity results in a family of injected charge at t=0 all with charge density q=l/?. As the charge propagates, Coulombi ...
... Approaching the x0=O, T=0 origin from along the axis has (x=0, 0-)=-, while approaching the origin from the t axis has E(x=0, t=0)=O for space charge limited conditions. This disgontinuity results in a family of injected charge at t=0 all with charge density q=l/?. As the charge propagates, Coulombi ...
cond-mat/0601319 PDF
... This statement finds strong confirmation in confinement phenomena of magnetic-dipolar oscillations. The dipole interaction provides us with a long-range mechanism of interaction, where a magnetic medium is considered as a continuum. Contrary to an exchange spin wave, in magneticdipolar waves the loc ...
... This statement finds strong confirmation in confinement phenomena of magnetic-dipolar oscillations. The dipole interaction provides us with a long-range mechanism of interaction, where a magnetic medium is considered as a continuum. Contrary to an exchange spin wave, in magneticdipolar waves the loc ...
Intermediate Algebra Summary
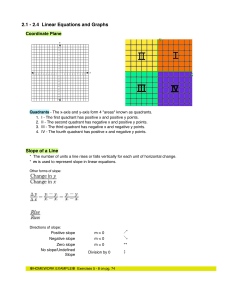
... A set of ordered pairs that assign to each xvalue exactly one y-value All functions are relations, but not all relations are functions. Linear equations are always functions Read “function of x” or “f of x” f(x) is another way of writing y Any linear equation that describes a function can be written ...
... A set of ordered pairs that assign to each xvalue exactly one y-value All functions are relations, but not all relations are functions. Linear equations are always functions Read “function of x” or “f of x” f(x) is another way of writing y Any linear equation that describes a function can be written ...
mathcad_homework_in_Matlab.m Dr. Dave S# Table of Contents
... Table of Contents Basic calculations - solution to quadratic equation: a*x^2 + b*x + c = 0 ....................................... 1 Plotting a function with automated ranges and number of points .................................................. 2 Plotting a function using a vector of values, with ...
... Table of Contents Basic calculations - solution to quadratic equation: a*x^2 + b*x + c = 0 ....................................... 1 Plotting a function with automated ranges and number of points .................................................. 2 Plotting a function using a vector of values, with ...
AP Calculus
... The “average” slope is the slope of a line drawn from endpoint to endpoint. No matter how much the function may change between endpoints, we say that its “average” change is simply the ratio of changes in y to changes in x. For average slope, use the slope formula. The MVT says that there has to be ...
... The “average” slope is the slope of a line drawn from endpoint to endpoint. No matter how much the function may change between endpoints, we say that its “average” change is simply the ratio of changes in y to changes in x. For average slope, use the slope formula. The MVT says that there has to be ...
IOSR Journal of Applied Physics (IOSR-JAP) e-ISSN: 2278-4861. www.iosrjournals.org
... this is because the Lagrangian is symmetric. It is a property which will be used in the following example. This example is a problem for which I have worked out the solution. Example 1 – Lagrangian in Hyperbolic Coordinates A particle is moving in the (x, y) plane where a force act on it towards the ...
... this is because the Lagrangian is symmetric. It is a property which will be used in the following example. This example is a problem for which I have worked out the solution. Example 1 – Lagrangian in Hyperbolic Coordinates A particle is moving in the (x, y) plane where a force act on it towards the ...
Chapter 7
... The numbers for which a rational expression is undefined are called the restrictions of the rational expression. In order to find the restrictions we must find the points that the rational expression’s denominator is equal to zero. We do this by creating a quadratic equation in standard form with t ...
... The numbers for which a rational expression is undefined are called the restrictions of the rational expression. In order to find the restrictions we must find the points that the rational expression’s denominator is equal to zero. We do this by creating a quadratic equation in standard form with t ...
Partial differential equation

In mathematics, a partial differential equation (PDE) is a differential equation that contains unknown multivariable functions and their partial derivatives. (A special case are ordinary differential equations (ODEs), which deal with functions of a single variable and their derivatives.) PDEs are used to formulate problems involving functions of several variables, and are either solved by hand, or used to create a relevant computer model.PDEs can be used to describe a wide variety of phenomena such as sound, heat, electrostatics, electrodynamics, fluid flow, elasticity, or quantum mechanics. These seemingly distinct physical phenomena can be formalised similarly in terms of PDEs. Just as ordinary differential equations often model one-dimensional dynamical systems, partial differential equations often model multidimensional systems. PDEs find their generalisation in stochastic partial differential equations.