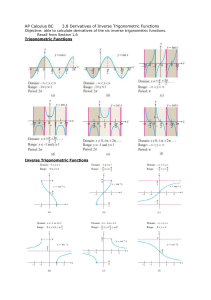
Chapter 4A: Linear Functions Index:
... convert from one unit to another in practical problems. In this situation we can almost always use proportional reasoning to do the job. In June, on the NYS CC Regents Exam you will be given a reference sheet. The top portion of the reference sheet is pictured to the right. This will help with any c ...
... convert from one unit to another in practical problems. In this situation we can almost always use proportional reasoning to do the job. In June, on the NYS CC Regents Exam you will be given a reference sheet. The top portion of the reference sheet is pictured to the right. This will help with any c ...
) (
... R( x) J n ( x), with J n ( x) (1) n J n ( x) and they have many nice properties (all documented in books). Generally speaking, the Bessel function is a complicated polynom. Let us now see using examples how we solve the Laplace equation in cylindrical coordinates. Exercise: A cylinder of radiu ...
... R( x) J n ( x), with J n ( x) (1) n J n ( x) and they have many nice properties (all documented in books). Generally speaking, the Bessel function is a complicated polynom. Let us now see using examples how we solve the Laplace equation in cylindrical coordinates. Exercise: A cylinder of radiu ...
10-3
... variables on both sides of the equal sign. Solving an equation with variables on both sides is similar to solving an equation with a variable on only one side. You can add or subtract a term containing a variable on both sides of an equation. ...
... variables on both sides of the equal sign. Solving an equation with variables on both sides is similar to solving an equation with a variable on only one side. You can add or subtract a term containing a variable on both sides of an equation. ...
Partial differential equation

In mathematics, a partial differential equation (PDE) is a differential equation that contains unknown multivariable functions and their partial derivatives. (A special case are ordinary differential equations (ODEs), which deal with functions of a single variable and their derivatives.) PDEs are used to formulate problems involving functions of several variables, and are either solved by hand, or used to create a relevant computer model.PDEs can be used to describe a wide variety of phenomena such as sound, heat, electrostatics, electrodynamics, fluid flow, elasticity, or quantum mechanics. These seemingly distinct physical phenomena can be formalised similarly in terms of PDEs. Just as ordinary differential equations often model one-dimensional dynamical systems, partial differential equations often model multidimensional systems. PDEs find their generalisation in stochastic partial differential equations.