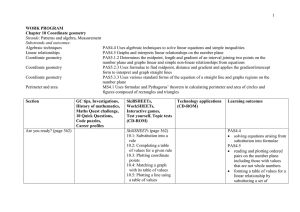
Caffeine in bloodstream (mg)
... Task 3 builds on students’ understandings of exponential functions and inverses to develop the idea of a logarithm. Through paper folding and examining graphs, students determine the graph of the inverse of an exponential function, eventually assigning the inverse the name logarithm. Students then w ...
... Task 3 builds on students’ understandings of exponential functions and inverses to develop the idea of a logarithm. Through paper folding and examining graphs, students determine the graph of the inverse of an exponential function, eventually assigning the inverse the name logarithm. Students then w ...
Bellwork/Spiral Review
... Review for Unit 2 Test Unit 2 Test Unit 3 Spiral Review: Teacher selected from Units 1, 2, HSAP and SAT/ACT. Lesson: 1) Use the discriminant to determine the number and type of solutions for a quadratic equation, 2) ...
... Review for Unit 2 Test Unit 2 Test Unit 3 Spiral Review: Teacher selected from Units 1, 2, HSAP and SAT/ACT. Lesson: 1) Use the discriminant to determine the number and type of solutions for a quadratic equation, 2) ...
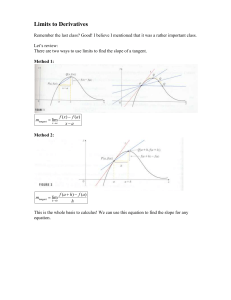
Limits to Derivatives
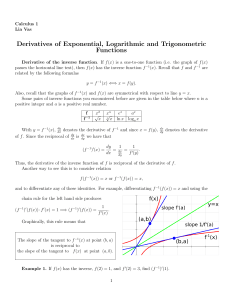
... derivative. The derivative is a function that represents the slope of a function at any point. We use two main ways to represent a function. The derivative of a function f(x) is f’(x) [we say: “f prime of x” or simply “the derivative of f”]. df (x) dy Another way to represent the derivative of the r ...
... derivative. The derivative is a function that represents the slope of a function at any point. We use two main ways to represent a function. The derivative of a function f(x) is f’(x) [we say: “f prime of x” or simply “the derivative of f”]. df (x) dy Another way to represent the derivative of the r ...
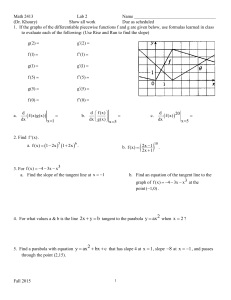
Lab 2
... 9. A curve C is defined by the parametric equations x t 2 , y t3 3t . a. Show that C has two tangents at the point c. Use your calculator to illustrate parts a and b (3,0) and find their equations. by graphing C and the tangent lines. ...
... 9. A curve C is defined by the parametric equations x t 2 , y t3 3t . a. Show that C has two tangents at the point c. Use your calculator to illustrate parts a and b (3,0) and find their equations. by graphing C and the tangent lines. ...
Partial differential equation

In mathematics, a partial differential equation (PDE) is a differential equation that contains unknown multivariable functions and their partial derivatives. (A special case are ordinary differential equations (ODEs), which deal with functions of a single variable and their derivatives.) PDEs are used to formulate problems involving functions of several variables, and are either solved by hand, or used to create a relevant computer model.PDEs can be used to describe a wide variety of phenomena such as sound, heat, electrostatics, electrodynamics, fluid flow, elasticity, or quantum mechanics. These seemingly distinct physical phenomena can be formalised similarly in terms of PDEs. Just as ordinary differential equations often model one-dimensional dynamical systems, partial differential equations often model multidimensional systems. PDEs find their generalisation in stochastic partial differential equations.