HCF AND LCM - bankexam.co.in
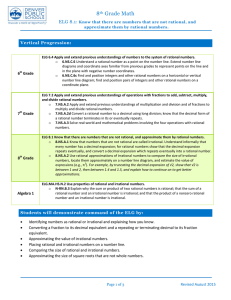
... (i) If the numbers are divided by their HCF, then relatively prime numbers are obtaiend as quotient. Hence, if the numbers be x and y and their HCF be m then x = ma and y - mb, where a and b are co-prime. (ii) When two numbers divided by a third number leave the same remainder, then the difference o ...
... (i) If the numbers are divided by their HCF, then relatively prime numbers are obtaiend as quotient. Hence, if the numbers be x and y and their HCF be m then x = ma and y - mb, where a and b are co-prime. (ii) When two numbers divided by a third number leave the same remainder, then the difference o ...
WE’VE GOT COOL MATH! MARCH 2013 CURIOUS MATHEMATICS FOR FUN AND JOY
... of parentheses? He assumed the parentheses were “freefloating.” For example, there is one way to arrange one pair: ( ), and there are two ways to arrange two pairs: ( ( ) ) and ( ) ( ). Comment: Do you see this is the same challenge as the opening stair-climbing puzzle? As one reads from left to rig ...
... of parentheses? He assumed the parentheses were “freefloating.” For example, there is one way to arrange one pair: ( ), and there are two ways to arrange two pairs: ( ( ) ) and ( ) ( ). Comment: Do you see this is the same challenge as the opening stair-climbing puzzle? As one reads from left to rig ...