When two lines cross, an angle is formed. Angles are measured in
... On the right, the two rays, AB and AC have the same endpoint and therefore form an angle. It is called a vertex. AB and AC are the sides of the angle. The small arrow indicates the angle that is being measured. The following notations can be used to refer to this angle. A or BAC or ...
... On the right, the two rays, AB and AC have the same endpoint and therefore form an angle. It is called a vertex. AB and AC are the sides of the angle. The small arrow indicates the angle that is being measured. The following notations can be used to refer to this angle. A or BAC or ...
0046_hsm11gmagp_0601.indd
... In this game, one student begins the chain by reading his or her “Who Has” question aloud and then waiting for the next participant to read the only “I Have” answer that correctly answers that question. Play continues until the first student reads his or her “I Have.” Materials Game strips (one se ...
... In this game, one student begins the chain by reading his or her “Who Has” question aloud and then waiting for the next participant to read the only “I Have” answer that correctly answers that question. Play continues until the first student reads his or her “I Have.” Materials Game strips (one se ...
Geometry A Unit 1 Day 6 Notes 1.5 Equal Parts of Segments and
... III. Group Practice: Answer the following questions the best you can. The answers are provided at the end of the section, in no particular order. If your group can not find your answer among those provided, ask your teacher to check your work. 1. In the diagram, AMN is bisected by MQ and RS bisect ...
... III. Group Practice: Answer the following questions the best you can. The answers are provided at the end of the section, in no particular order. If your group can not find your answer among those provided, ask your teacher to check your work. 1. In the diagram, AMN is bisected by MQ and RS bisect ...
Click Here to View My Lesson
... Has three sides and vertices Sum of interior angles = 180° Types of Triangles: ...
... Has three sides and vertices Sum of interior angles = 180° Types of Triangles: ...
Geometric Figures - U of L Class Index
... If you look carefully, you will see that the bond angle is more than 90°. You can also see that the four blue atoms are not in the same plane. Two of the blue atoms are much smaller than the other two blue atoms because, in space, they are behind the larger blue atoms. This kind of molecule is NOT p ...
... If you look carefully, you will see that the bond angle is more than 90°. You can also see that the four blue atoms are not in the same plane. Two of the blue atoms are much smaller than the other two blue atoms because, in space, they are behind the larger blue atoms. This kind of molecule is NOT p ...
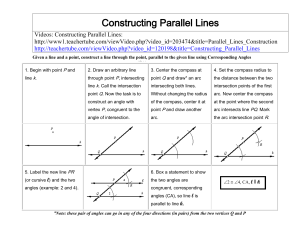
4.Get Organize d Compare the Corresponding Angles P ostulate
... Copyright © by Holt, Rinehart and Winston. All rights reserved. ...
... Copyright © by Holt, Rinehart and Winston. All rights reserved. ...
Triangle Similarity
... equal, then the third angle must also be equal, because angles of a triangle always add to make 180°. In this case the missing angle is: ...
... equal, then the third angle must also be equal, because angles of a triangle always add to make 180°. In this case the missing angle is: ...
Euler angles
The Euler angles are three angles introduced by Leonhard Euler to describe the orientation of a rigid body. To describe such an orientation in 3-dimensional Euclidean space three parameters are required. They can be given in several ways, Euler angles being one of them; see charts on SO(3) for others. Euler angles are also used to describe the orientation of a frame of reference (typically, a coordinate system or basis) relative to another. They are typically denoted as α, β, γ, or φ, θ, ψ.Euler angles represent a sequence of three elemental rotations, i.e. rotations about the axes of a coordinate system. For instance, a first rotation about z by an angle α, a second rotation about x by an angle β, and a last rotation again about z, by an angle γ. These rotations start from a known standard orientation. In physics, this standard initial orientation is typically represented by a motionless (fixed, global, or world) coordinate system; in linear algebra, by a standard basis.Any orientation can be achieved by composing three elemental rotations. The elemental rotations can either occur about the axes of the fixed coordinate system (extrinsic rotations) or about the axes of a rotating coordinate system, which is initially aligned with the fixed one, and modifies its orientation after each elemental rotation (intrinsic rotations). The rotating coordinate system may be imagined to be rigidly attached to a rigid body. In this case, it is sometimes called a local coordinate system. Without considering the possibility of using two different conventions for the definition of the rotation axes (intrinsic or extrinsic), there exist twelve possible sequences of rotation axes, divided in two groups: Proper Euler angles (z-x-z, x-y-x, y-z-y, z-y-z, x-z-x, y-x-y) Tait–Bryan angles (x-y-z, y-z-x, z-x-y, x-z-y, z-y-x, y-x-z). Tait–Bryan angles are also called Cardan angles; nautical angles; heading, elevation, and bank; or yaw, pitch, and roll. Sometimes, both kinds of sequences are called ""Euler angles"". In that case, the sequences of the first group are called proper or classic Euler angles.