Test 1 Plan
... right-angled but not equilateral; a rhombus that which is equilateral but not right-angled; and a rhomboid that which has its opposite sides and angles equal to one another but is neither equilateral nor right-angled. And let quadrilaterals other than these be called trapezia. Definition 23 Parallel ...
... right-angled but not equilateral; a rhombus that which is equilateral but not right-angled; and a rhomboid that which has its opposite sides and angles equal to one another but is neither equilateral nor right-angled. And let quadrilaterals other than these be called trapezia. Definition 23 Parallel ...
CPCTC Lesson.notebook
... Explain the differences between acute, obtuse, right and straight angles. Draw and label one of each. ...
... Explain the differences between acute, obtuse, right and straight angles. Draw and label one of each. ...
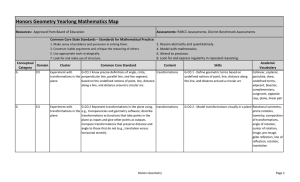
Honors Geometry Yearlong Curriculum Map
... angle to those that do not (e.g., translation versus horizontal stretch). Experiment with G-CO.2 Represent transformations in the plane using, transformations transformations in the e.g., transparencies and geometry software; describe plane transformations as functions that take points in the plane ...
... angle to those that do not (e.g., translation versus horizontal stretch). Experiment with G-CO.2 Represent transformations in the plane using, transformations transformations in the e.g., transparencies and geometry software; describe plane transformations as functions that take points in the plane ...
Not Polygons
... The cloud of water leaving a whale’s blowhole when it exhales is called its blow. A biologist observed blue-whale blows of 25 ft, 29 ft, 27 ft, and 24 ft. Another biologist recorded humpback-whale blows of 8 ft, 7 ft, 8 ft, and 9 ft. Make a conjecture based on the data. ...
... The cloud of water leaving a whale’s blowhole when it exhales is called its blow. A biologist observed blue-whale blows of 25 ft, 29 ft, 27 ft, and 24 ft. Another biologist recorded humpback-whale blows of 8 ft, 7 ft, 8 ft, and 9 ft. Make a conjecture based on the data. ...
3.2 Exterior Angles of a Triangle
... When a transversal intersects two lines, four pairs of opposite angles are formed. The angles in each pair are equal. When the lines are parallel, angles in other pairs are also equal. We can use tracing paper to show these relationships. Corresponding angles are equal. They have the same position w ...
... When a transversal intersects two lines, four pairs of opposite angles are formed. The angles in each pair are equal. When the lines are parallel, angles in other pairs are also equal. We can use tracing paper to show these relationships. Corresponding angles are equal. They have the same position w ...
Euler angles
The Euler angles are three angles introduced by Leonhard Euler to describe the orientation of a rigid body. To describe such an orientation in 3-dimensional Euclidean space three parameters are required. They can be given in several ways, Euler angles being one of them; see charts on SO(3) for others. Euler angles are also used to describe the orientation of a frame of reference (typically, a coordinate system or basis) relative to another. They are typically denoted as α, β, γ, or φ, θ, ψ.Euler angles represent a sequence of three elemental rotations, i.e. rotations about the axes of a coordinate system. For instance, a first rotation about z by an angle α, a second rotation about x by an angle β, and a last rotation again about z, by an angle γ. These rotations start from a known standard orientation. In physics, this standard initial orientation is typically represented by a motionless (fixed, global, or world) coordinate system; in linear algebra, by a standard basis.Any orientation can be achieved by composing three elemental rotations. The elemental rotations can either occur about the axes of the fixed coordinate system (extrinsic rotations) or about the axes of a rotating coordinate system, which is initially aligned with the fixed one, and modifies its orientation after each elemental rotation (intrinsic rotations). The rotating coordinate system may be imagined to be rigidly attached to a rigid body. In this case, it is sometimes called a local coordinate system. Without considering the possibility of using two different conventions for the definition of the rotation axes (intrinsic or extrinsic), there exist twelve possible sequences of rotation axes, divided in two groups: Proper Euler angles (z-x-z, x-y-x, y-z-y, z-y-z, x-z-x, y-x-y) Tait–Bryan angles (x-y-z, y-z-x, z-x-y, x-z-y, z-y-x, y-x-z). Tait–Bryan angles are also called Cardan angles; nautical angles; heading, elevation, and bank; or yaw, pitch, and roll. Sometimes, both kinds of sequences are called ""Euler angles"". In that case, the sequences of the first group are called proper or classic Euler angles.