Degrees, Radians and Revolutions
... In algebra 2 and precalculus, students learn and make use of the conversion between degrees and radians, but often lose sight of the most important feature of radians—that their purpose is to allow you to easily determine the arc length (distance traveled around the circle) by simply multiplying the ...
... In algebra 2 and precalculus, students learn and make use of the conversion between degrees and radians, but often lose sight of the most important feature of radians—that their purpose is to allow you to easily determine the arc length (distance traveled around the circle) by simply multiplying the ...
SSS,SAS,ASA,AAS notes.notebook
... If two angles and a nonincluded side in one triangle are congruent to two angles and the corresponding nonincluded side in another triangle, then the triangles are congruent ...
... If two angles and a nonincluded side in one triangle are congruent to two angles and the corresponding nonincluded side in another triangle, then the triangles are congruent ...
FOUNDATIONS OF ALGEBRA
... Summarize the structure and relationship between undefined terms, defined terms, axioms/postulates, methods of reasoning and theorems. Explain the relationships among angles formed by perpendicular lines and transversals of parallel lines. Use paper-folding techniques, compasses and straight edges a ...
... Summarize the structure and relationship between undefined terms, defined terms, axioms/postulates, methods of reasoning and theorems. Explain the relationships among angles formed by perpendicular lines and transversals of parallel lines. Use paper-folding techniques, compasses and straight edges a ...
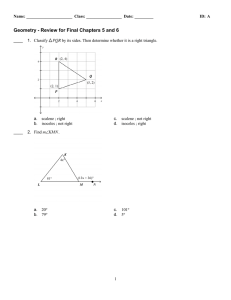
ExamView - geometry review for final chapters 5 and 6 .tst
... 53. A pet owner plans to tie up the dog so it can reach the places shown in the diagram. Explain how the owner can determine where to place a stake so that it is the same distance from the dog’s food, the doghouse, and the door to the owner’s house. ...
... 53. A pet owner plans to tie up the dog so it can reach the places shown in the diagram. Explain how the owner can determine where to place a stake so that it is the same distance from the dog’s food, the doghouse, and the door to the owner’s house. ...
Euler angles
The Euler angles are three angles introduced by Leonhard Euler to describe the orientation of a rigid body. To describe such an orientation in 3-dimensional Euclidean space three parameters are required. They can be given in several ways, Euler angles being one of them; see charts on SO(3) for others. Euler angles are also used to describe the orientation of a frame of reference (typically, a coordinate system or basis) relative to another. They are typically denoted as α, β, γ, or φ, θ, ψ.Euler angles represent a sequence of three elemental rotations, i.e. rotations about the axes of a coordinate system. For instance, a first rotation about z by an angle α, a second rotation about x by an angle β, and a last rotation again about z, by an angle γ. These rotations start from a known standard orientation. In physics, this standard initial orientation is typically represented by a motionless (fixed, global, or world) coordinate system; in linear algebra, by a standard basis.Any orientation can be achieved by composing three elemental rotations. The elemental rotations can either occur about the axes of the fixed coordinate system (extrinsic rotations) or about the axes of a rotating coordinate system, which is initially aligned with the fixed one, and modifies its orientation after each elemental rotation (intrinsic rotations). The rotating coordinate system may be imagined to be rigidly attached to a rigid body. In this case, it is sometimes called a local coordinate system. Without considering the possibility of using two different conventions for the definition of the rotation axes (intrinsic or extrinsic), there exist twelve possible sequences of rotation axes, divided in two groups: Proper Euler angles (z-x-z, x-y-x, y-z-y, z-y-z, x-z-x, y-x-y) Tait–Bryan angles (x-y-z, y-z-x, z-x-y, x-z-y, z-y-x, y-x-z). Tait–Bryan angles are also called Cardan angles; nautical angles; heading, elevation, and bank; or yaw, pitch, and roll. Sometimes, both kinds of sequences are called ""Euler angles"". In that case, the sequences of the first group are called proper or classic Euler angles.