Download Student Guide - Math Site

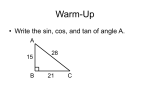
Name:_________________________________________ Date: _______________________ Period:____________
Advanced Algebra, Unit 7: Trigonometric Functions
Lesson Title
Content Objectives
Language Objectives
Learning
Standards
DP
Compet
encies
M01.
M03.
Time
(Days)
7.1 Pythagorean
Theorem and
Special Right
Triangles
*remedial
7.2: Right
Triangles and
Trigonometry
SWBAT find missing sides of
right triangles using
Pythagorean Theorem and
ratios of special right triangles.
SWBAT analyze how the
Pythagorean Theorem can
be used to derive the ratios
for a 45-45-90 right triangle.
G-SRT.8
SWBAT define trigonometric
ratios and solve problems
involving right triangles.
7.3: Law of Sines
and Cosines
SWBAT use trigonometric
functions to solve problems
involving non-right triangles.
7.4: Degrees,
Radians, and the
Unit Circle
SWBATconstruct angles on a
coordinate plan and use
trigonometric function to
calculate angle measures and
convert between radians and
degrees.
7.5: Graphing and
Modeling with
Trigonometric
Functions
SWBAT analyze, graph, and
model with trigonometric
functions, showing period,
midline, and amplitude.
SWBAT analyze the
relationship between sine
and cosine and justify their
analysis with and example of
their own.
SWBAT create a real-world
problem involving a nonright triangles that they
cannot solve with the Law of
Sines, and then justify why
they do not have sufficient
information to solve the
problem.
SWBAT construct a
paragraph explaining how
to properly measure angles
on the x-y coordinate plane
using radians. Students will
include vocabulary words
standard position, initial
side, and terminal side.
SWBAT analyze what
alterations to a trigonometric
function affect the period and
amplitude of the function and
explain how to calculate the
period and amplitude from
the transformed function.
G-SRT.6
G-SRT.7
G-SRT.8
M01.
M03.
2
G-SRT.6
G-SRT.7
M01.
M03.
2
F-TF.1
F-TF.2
M01.
M03.
2
F-IF.7e
F-BF.3
F-TF.5
M01.
M03.
2
Lesson 7.1: Pythagorean Theorem and Special Right Triangles
Conent Objective: SWBAT find missing sides of right triangles using Pythagorean Theorem and ratios of special right
triangles.
Diploma Plus Competencies: M01. Problem Solving; M03. Quantitative Reasoning,
Pythagorean Theorem
For any right triangle with legs (short sides) a and b and hypotenuse (longest side) c: 𝑎 2
+ 𝑏2 = 𝑐 2.
PRACTICE:
45° - 45° - 90° Special Right Triangle
The first type of special triangle is an isosceles right triangle. Recall that an
isosceles triangle has two angles that are congruent and two sides that are
congruent. Notice that the two legs of the triangle will be congruent. If one
leg is
X units long the other leg will also be X units long. The length of the hypotenuse can be found by multiplying the length
of a leg, X units, by √2.
PRACTICE:
30° - 60° - 90° Special Right Triangle
The second type of special triangle is a30° - 60° - 90° Special Right Triangle. If
we label the shortest side (opposite the 30° angle) of this special triangle X
units then we can use this one measurement to find the remaining sides. The
middle length leg (opposite the 60° angle) will be 𝑋√3 units long, and the
hypotenuse (opposite the 90° angle) will be 2X units long.
PRACTICE:
Higher Level Thinking Questions:
Language Objective: SWBAT analyze how the Pythagorean Theorem can be used to derive the ratios for a
45-45-90 right triangle.
Write a paragraph explaining how to the ratios for a 45-45-90 Right Triangle can be found using the
Pythagorean Theorem. Include an explanation of how the 45 degree angles are important to deriving the
ratios as well.
Lesson 7.2: Right Triangle Trigonometry
Objective: SWBAT define trigonometric ratios and solve problems involving right triangles.
Diploma Plus Competencies: M01. Problem Solving; M03. Quantitative Reasoning,
Recall that a right triangle is a triangle with exactly one right (90 degree) angle. The sides and angles of right
triangles have a predictable relationship that can be quantified using Trigonometric Functions.
Trigonometric Functions
A trigonometric function is a function with an input and an output. The input is an ANGLE MEASURE and the output is a
RATIO OF SIDES. Fill in the missing information for the three trigonometric functions. (Refer to page 440 in Discovering
Advanced Algebra for help.)
Angle A
SINE of angle A is ___________________________________________________________________________
sin A 

COSINE of angle A is ________________________________________________________________________
cos A 

TANGENT of angle A is _______________________________________________________________________
tan A 

INVERSE TRIGONOMETRIC FUNCTIONS also have an input and an output. The input for the inverse trigonometric
functions is a RATIO of SIDES and the output is an ANGLE MEASURE.
a
sin 1    measure of angle A
c

cos 1 


 
  measure of angle A tan 1    measure of angle A

 
Inverse Trigonometric Functions are used to solve problems where we know two of the sides of a right triangle and we
want to find one of the missing angles. They are also used to “undo” a trigonometric function when solving an equation
with an unknown angle measure in the as the input to a trigonometric function.
PRACTICE:Discovering Advanced AlgebraPage443 - 446; #1, 2, 3, 4, 12
For additional support please see the resources section of Summit’s Math Site.
Higher Level Thinking Questions:
Language Objective: SWBAT analyze the relationship between sine and cosine and justify their analysis
with and example of their own.
Find the corresponding ratios for the following trigonometric functions:
sin(30°) =
cos(60°) =
sin(75°) =
cos(15°) =
Write a paragraph explaining what pattern you notice in the answers that you found? Create and write a
rule based on the pattern that you discovered and give another example to justify your rule.
Lesson 7.3: Law of Sines and Cosines
Objective: SWBAT use trigonometric functions to solve problems involving non-right triangles.
Diploma Plus Competencies: M01. Problem Solving; M03. Quantitative Reasoning,
Trigonometric ratios are very helpful in helping us find missing angles and side lengths for right triangles,
but many triangles do not have right angles. We can still use the sine and cosine function to help use
solve for missing parts of any triangle. We will start by looking at the Law of Sines (pronounced “signs”).
Law of Sines
For any triangle, the ratios of each angle and its opposite side are
equal. This is easily seen in the diagram below.
sin 𝐴
𝑎
=
sin 𝐵
𝑏
=
sin 𝐶
𝑐
Note: Only two ratios are needed to solve for a missing side or
angle, not all three ratios.
Ex:
Find the measure of side c.
This is a straight forward Law of Sines problem where
we simply need to plug in the values we have and find
the missing value.
sin 𝐴
𝑎
=
sin 𝐶
𝑐
sin 43
4.56
=
sin 57
𝑐
solve for the missing value c.
c = 5.61
PRACTICE:Discovering Advanced AlgebraPage472 - 475; #1 - 4, 6, 8
For additional support please see the resources section of Summit’s Math Site.
Higher Level Thinking Questions:
Language Objective: SWBAT create a real-world problem involving a non-right triangles that they cannot
solve with the Law of Sines, and then justify why they do not have sufficient information to solve the
problem.
Create a real-world problem that involves a non-right triangle with a missing side or angle that cannot be
solved using the Law of Sines. Justify why the problem you created is unsolvable with the knowledge you
have so far.
Law of Cosines
If you completed the Higher Level Thinking Question above you see how there are some triangle problems that we
cannot solve using trigonometry or Law of Sines. For those problems we use the Law of Cosines.
Use on of the following equations based on the information given.
𝑎2 = 𝑏 2 + 𝑐 2 − 2 ∙ 𝑏 ∙ 𝑐 ∙ cos 𝐴
𝑏 2 = 𝑎2 + 𝑐 2 − 2 ∙ 𝑎 ∙ 𝑐 ∙ cos 𝐵
𝑐 2 = 𝑎2 + 𝑏 2 − 2 ∙ 𝑎 ∙ 𝑏 ∙ cos 𝐶
Or
Or
Note how close the Law of Cosines is to the Pythagorean Theorem; it is
adjusted by a factor of the cosine of the known angle.
Ex:
Find the length of side r from the given diagram to the right.
Notice that with two sides and the included angle we cannot use the Law of
Sines to find r. We will instead use the Law of Cosines to find r.
𝑟2 =
𝑟2 =
𝑟2 =
𝑟 =
𝑝2 + 𝑞 2 − 2 ∙ 𝑝 ∙ 𝑞 ∙ cos 𝑅
6.52 + 7.42 − 2 ∙ 6.5 ∙ 7.4 ∙ cos 58
46.03
6.78
PRACTICE:Discovering Advanced AlgebraPage479 - 482; #1, 2, 4, 8
For additional support please see the resources section of Summit’s Math Site.
Lesson 7.4: Degrees, Radians, and the Unit Circle
Objective: SWBAT construct angles on a coordinate plan and use trigonometric function to calculate angle measures
and convert between radians and degrees.
Diploma Plus Competencies: M01. Problem Solving; M03. Quantitative Reasoning,
There are two common units of measurement for angles. You are already familiar with measuring angles
with degrees but we learn in this lesson about radians and how radians and degrees are related through
the Unit Circle. We will start with a more in depth look at angles.
Angles
We will be working with angles that are placed on the
x-y coordinate plane with the vertex of the angle
centered at the origin.
Whenever we have a problem that involves an angle
think of the angle of the x-y plane and then place the
angle in Standard Position.
Standard position is when the vertex of the angle is at
the origin, and one of the sides of the angle is on the
positive side of the x-axis (also called the initial side).
The other side of the angle can be in any of the 4
quadrants and is called the terminal side. The graph
to the right shows an angle in standard position.
Angles are always measured counter-clockwise from the initial side to the terminal side. If you measure
an angle clockwise then the angle measurement will be negative.
PRACTICE: Algebra 2: Concepts and SkillsPage656 - 657; # 3 – 6, 16 - 18
For additional support please see the resources section of Summit’s Math Site.
When an angle is in standard position we can use
trigonometric functions and a point of the terminal side
of the angle to find the unknown angle measurement.
Ex:
Let (-5, -4) be a point on the terminal side of an
angle A is standard position. Find the
measurement
of angle A in degrees.
The first step is to draw the angle on the x-y plane
in standard position.
With the angle in standard position we can
construct a right angle using the terminal side
and the negative side of the x-axis. The dotted lines on
the graph show us the legs of the right
triangle
with length 5 and 4.
We can use these legs, which are the opposite and
inverse tangent function to calculate the measure of the angle
and the terminal side of A.
adjacent legs, and the
Abetween the negative x-axis
4
𝑡𝑎𝑛−1 5 = 𝐴 ≈ 39°
Remember that we measure an angle counter-clockwise from the initial side to the terminal side.
We know that from the initial side to the negative x-axis is 180°, therefore the measure of angle A
is 180° + 39° = 219°
PRACTICE:Algebra 2: Concepts and SkillsPage 657; # 37 – 39 find 𝜃
For additional support please see the resources section of Summit’s Math Site.
Radians
Instead of describing the size of an angle using
degrees we can use radians. A radian is derived
from a circle with radius equal to 1 unit. If the radius
of a circle is 1 unit then the circumference of that
circle will be C = 2r𝜋 = 2(1)𝜋 = 2𝜋. So instead of
calling a complete rotation around a circle 360° we
will call a full rotation 2𝜋 radians.
The diagram to the right is called the Unit Circle. The
Unit Circle has a radius of exactly 1 unit and it shows
us the relationship between radians and degrees. We
can also use the conversion equation below to change
from degrees to radians and vice versa.
𝑎𝑛𝑔𝑙𝑒 𝑖𝑛 𝑑𝑒𝑔𝑟𝑒𝑒𝑠
𝑎𝑛𝑔𝑙𝑒 𝑖𝑛 𝑟𝑎𝑑𝑖𝑎𝑛𝑠
=
360°
2𝜋
PRACTICE:Discovering Advanced AlgebraPage 578 - 579; #1, 4, 5
For additional support please see the resources section of Summit’s Math Site.
Higher Level Thinking Questions:
Language Objective: SWBAT construct a paragraph explaining how to properly measure angles on the x-y
coordinate plane using radians. Students will include vocabulary words standard position, initial side, and
terminal side.
Construct a paragraph explaining how to properly measure angles on the x-y coordinate plane using
radians. Include the vocabulary words standard position, initial side, and terminal side in your
explanation.
Lesson 7.5: Graphing and Modeling with Trigonometric Functions
Objective: SWBAT analyze, graph, and model with trigonometric functions, showing period, midline, and amplitude.
Diploma Plus Competencies: M01. Problem Solving; M03. Quantitative Reasoning,
Remember that sine and cosine are functions that take an angle measure (degrees or radians) as an input
and give a ratio of sides as an output. We can graph these trigonometric functions of the x-y plane.
PRACTICE:
1) Graph 𝑦 = sin 𝑥 on a graphing calculator and write a paragraph describing the graph. Make sure to
include the shape, the y-intercept, any x-intercepts, and any pattern that you notice.
2) Graph 𝑦 = cos 𝑥 on a graphing calculator and write a paragraph describing the graph. Make sure to
include the shape, the y-intercept, any x-intercepts, and any pattern that you notice.
The shape of the sine and cosine function is called a wave or a sinusoid. These waves have two
distinguishing features: the amplitude and the period.
Amplitude – the height of a wave. The amplitude of y = sin x is 1.
Period –
𝑚𝑎𝑥𝑖𝑚𝑢𝑚 𝑜𝑓 𝑤𝑎𝑣𝑒 − 𝑚𝑖𝑛𝑖𝑚𝑢𝑚 𝑜𝑓 𝑤𝑎𝑣𝑒
2
the frequency of the wave or the length of one wave before it repeats. The period of y = sin
x is 2𝜋 radians or 360°.
PRACTICE:
1) Find the period and amplitude for the following trigonometric functions:
a) 𝑦 = cos 𝑥
b) 𝑦 = 2 sin 𝑥
𝑥
c) 𝑦 = cos 2
Trigonometric functions can be transformed the same way we transformed functions in semester one. In the
𝑥−ℎ
following practice problems use trigonometric functions of the form 𝑦 = 𝑘 + 𝑏 𝑠𝑖𝑛( 𝑎 ).
PRACTICE:Discovering Advanced AlgebraPage 589 - 592; #1, 3, 5, 7, 8
For additional support please see the resources section of Summit’s Math Site.
Higher Level Thinking Questions:
Language Objective: SWBAT analyze what alterations to a trigonometric function affect the period and amplitude of the
function and explain how to calculate the period and amplitude from the transformed function.
Write a paragraph analyzing what alterations to a trigonometric function affect the period and amplitude of the function
and explain how to calculate the period and amplitude from the transformed function.