DIFFERENTIAL GEOMETRY HW 3 32. Determine the dihedral
... (d): Show that the Seifert-Weber space is a manifold at the vertex. Proof. To do so, we must show that a neighborhood of the vertex is a ball. At each vertex on the dodecahedron, draw oriented edges connecting the edges that meet at that vertex, labeled appropriately. In so doing, we end up with 20 ...
... (d): Show that the Seifert-Weber space is a manifold at the vertex. Proof. To do so, we must show that a neighborhood of the vertex is a ball. At each vertex on the dodecahedron, draw oriented edges connecting the edges that meet at that vertex, labeled appropriately. In so doing, we end up with 20 ...
Vocabulary - Hartland High School
... THEOREM 4.8: CONVERSE OF BASE ANGLES THEOREM If two angles of a triangle are congruent, then the sides opposite them are congruent. ...
... THEOREM 4.8: CONVERSE OF BASE ANGLES THEOREM If two angles of a triangle are congruent, then the sides opposite them are congruent. ...
Review Geometry common assessment 4 Printable
... 17. Three vertices of a kite are drawn at coordinates ...
... 17. Three vertices of a kite are drawn at coordinates ...
File
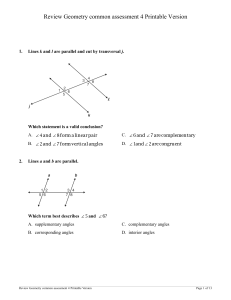
... Use the following diagram and the fact that line a is not parallel to line b to complete the statement. t (3x – 15) (5x – 57) ...
... Use the following diagram and the fact that line a is not parallel to line b to complete the statement. t (3x – 15) (5x – 57) ...
7.1 Triangle Application Theorems
... triangles is 180. • The measure of an exterior angles of a triangles is equal to the sum of the measures of the remote interior angles. • If a segment joining the midpoints of two sides of a triangle is parallel to the third side, then its length is one-half the length of the third side (Midline The ...
... triangles is 180. • The measure of an exterior angles of a triangles is equal to the sum of the measures of the remote interior angles. • If a segment joining the midpoints of two sides of a triangle is parallel to the third side, then its length is one-half the length of the third side (Midline The ...
PHƯƠNG PHÁP PHÁT HIỆN CÁC ĐỊNH LÍ MỚI VỀ HÌNH HỌC
... To find out new theorems in general and new geometric theorems in particular is all of our dream. That’s reason why, researchers give not only nice and beautiful theorems but also founded methods of new geometric theorems. These are two important factors of researchers in this era. In fact, there ar ...
... To find out new theorems in general and new geometric theorems in particular is all of our dream. That’s reason why, researchers give not only nice and beautiful theorems but also founded methods of new geometric theorems. These are two important factors of researchers in this era. In fact, there ar ...
Coord Alg–EOCT Review Powerpoint
... 62) For an arithmetic sequence a1 = 21, the recursive formula is an = an-1+11. Which explicit formula can be used to find the nth term in the sequence? A) an = 10 – 11n B) an = 10 + 11n ...
... 62) For an arithmetic sequence a1 = 21, the recursive formula is an = an-1+11. Which explicit formula can be used to find the nth term in the sequence? A) an = 10 – 11n B) an = 10 + 11n ...
NM3M04GAA.pdf
... If two sides of a triangle are congruent, then the angles opposite them are congruent. If AB AC , then B ________ ...
... If two sides of a triangle are congruent, then the angles opposite them are congruent. If AB AC , then B ________ ...
Steinitz's theorem

In polyhedral combinatorics, a branch of mathematics, Steinitz's theorem is a characterization of the undirected graphs formed by the edges and vertices of three-dimensional convex polyhedra: they are exactly the (simple) 3-vertex-connected planar graphs (with at least four vertices). That is, every convex polyhedron forms a 3-connected planar graph, and every 3-connected planar graph can be represented as the graph of a convex polyhedron. For this reason, the 3-connected planar graphs are also known as polyhedral graphs. Steinitz's theorem is named after Ernst Steinitz, who submitted its first proof for publication in 1916. Branko Grünbaum has called this theorem “the most important and deepest known result on 3-polytopes.”The name ""Steinitz's theorem"" has also been applied to other results of Steinitz: the Steinitz exchange lemma implying that each basis of a vector space has the same number of vectors, the theorem that if the convex hull of a point set contains a unit sphere, then the convex hull of a finite subset of the point contains a smaller concentric sphere, and Steinitz's vectorial generalization of the Riemann series theorem on the rearrangements of conditionally convergent series.↑ ↑ 2.0 2.1 ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑